Chapter 1.3 Homework

1. The graph of the following function is shifted upward by 6 units. 

$f\left(x\right)=x^2$

Write an equation for this translation. y=

 

2. Write a formula for the function g(x) obtained when the graph of 

$f\left(x\right)=\sqrt{x}$

  is shifted up 1 unit and to the left 6 units.

$g\left(x\right)=$

 

3. The graph of the basic function

$y=\sqrt{x}$

undergoes two successive transformations. The equation of the transformed graph is

$y=\sqrt{x–6}–9$

 

Select these two transformations from the list below. (Select all that apply.)

1. shifted to the left 6 units
2. shifted up 9 units
3. reflected about the y-axis
4. shifted down 9 units
5. reflected about the x-axis
6. shifted to the right 6 units

 

4.  Describe how the graph of the function is a transformation of the graph of the original function f.

$y=f\left(x–54\right)$

1. The graph of y = f(x − 54) is a horizontal shift to the left 54 units of the graph of f.
2. The graph of y = f(x − 54) is a vertical shift up 54 units of the graph of f
3. The graph of y = f(x − 54) is a vertical shift down 54 units of the graph of f.
4. The graph of y = f(x − 54) is a horizontal shift to the right 54 units of the graph of f.

 

5.  Determine the interval(s) on which the function is increasing and decreasing. (Enter your answers using interval notation. If an answer does not exist, enter DNE.)

$f\left(x\right)=8{\left(x+9\right)}^2–5$

Increasing

Decreasing

 

6.  Sketch a graph of the function as a transformation of the graph of one of the toolkit functions.

$m\left(t\right)=3+\sqrt{t+4}$

 

7.  Consider the graph of 

$y=f\left(x\right)$

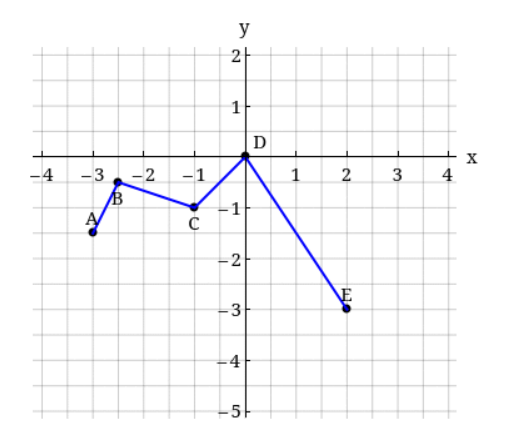
Which of the following is the graph of 

$y=3f\left(x\right)$

 

8.  The graph of 

$y=f\left(x\right) is shown below$

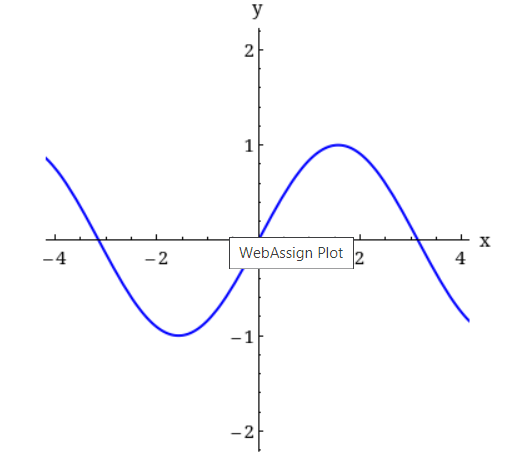
Sketch the graph of

$y=f\left(–x\right)$

 

9.  What is the equation of the square root function in the graph?

$y=\sqrt{x–1}+3$

 

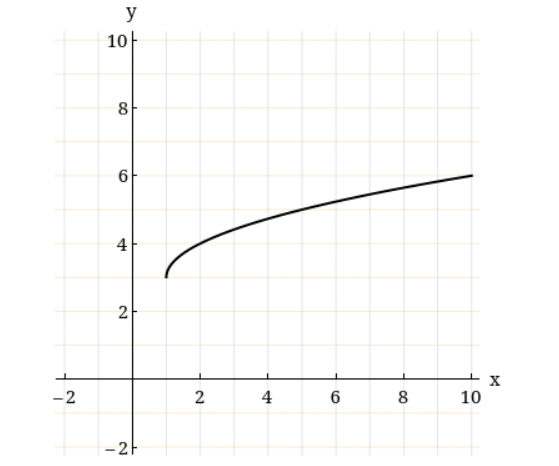
10.  The function of

$y=\sqrt{\frac{1}{6}x }$

is a transformation of 

$y=\sqrt{x}$

.  Which of the following statements describes this transformation?

1. compressed vertically by a factor of 6
2. shifted 6 units left    
3. shifted 6 units up
4. stretched horizontally by a factor of 6

 

11. Describe the transformation from the graph of

$y=\sqrt{x+2}$

to the graph of 

$y=–\sqrt{x+2}$

1. reflected about the x-axis
2. reflected about the y-axis
3. reflected about the line y = x

 

12 Describe how the graph of the function is a transformation of the graph of the original function f.

$g\left(x\right)=–f\left(x\right)$

The graph of g is a _______  reflection (across the _____) of the graph of f.

 

13.  Describe how the graph of the function is a transformation of the graph of the original function f. 

$g\left(x\right)=f\left(–x\right)$

The graph of g is a _______  reflection (across the _____) of the graph of f.

 

14. Describe how the graph of the function is a transformation of the graph of the original function f.

$g\left(x\right)=7f\left(x\right)$

The graph of g is a _______  reflection by a factor of _____ of the graph of f.

 

15.  Describe how the graph of the function is a transformation of the graph of the original function f.

$g\left(x\right)=f\left(6x\right)$

The graph of g is a _______  reflection by a factor of _____ of the graph of f.

 

16.  The graph of  

$y=\sqrt{x}$

    is compressed vertically by a factor of  

$\frac{1}{6}$

.      Write an equation for this transformed graph.

 

17.   You are given the graph of the function 

$y=\left|x\right|$

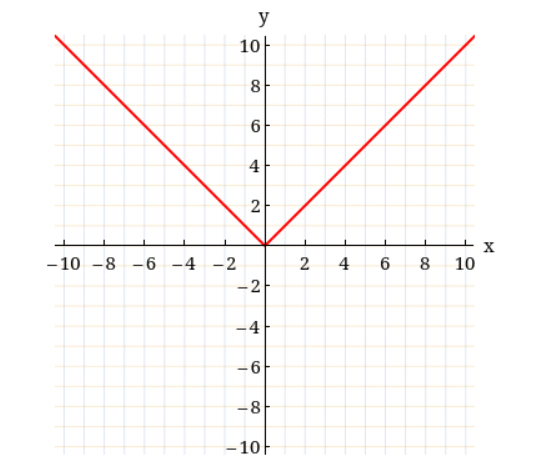
This graph is then transformed in the following ways.

1. It is first compressed horizontally by a factor of 4
2. It is then reflected about the x-axis

Which of the following shows the graph after these transformations are applied?

 

18  Write a formula for the function g that results when the graph of a given toolkit function is transformed as described.

The graph of 

$f\left(x\right)=\left|x\right|$

   is reflected over the y-axis and horizontally compressed by a factor of 

$\frac{1}{7}$

$g\left(x\right)$

=

 

19.  Write a formula for the function g that results when the graph of a given toolkit function is transformed as described.

The graph of 

$f\left(x\right)=\sqrt{x}$

  is reflected over the x-axis and horizontally stretched by a factor of 5.

$g\left(x\right)$

=

 

20.  Write a formula for the function g that results when the graph of a given toolkit function is transformed as described.

The graph of 

$f\left(x\right)=x^2$

   is vertically compressed by a factor of 

$\frac{1}{7}$

   then shifted to the right 6 units and up 1 unit.

$g\left(x\right)=$

 

21.  Describe how the formula is a transformation of a toolkit function.

$p\left(x\right)={\left(\frac{1}{4}x\right)}^3–4$

1. p(x) is stretched vertically by a factor of 4 and then shifted down 4 units.
2. p(x) is compressed horizontally by a factor of 4 and then shifted down 4 units. 
3. p(x) is compressed horizontally by a factor of 4 and then shifted up 4 units.
4. p(x) is stretched horizontally by a factor of 4 and then shifted up 4 units.
5. p(x) is stretched horizontally by a factor of 4 and then shifted down 4 units.

 

22  Suppose the graph of f is given. Write an equation for each graph described that is obtained from the graph of f.

1. Shift 8 units upward.
2. Shift 8 units downward
3. Shift 8 units to the right
4. Shift 8 units to the left.
5. Reflect about the x-axis
6. Reflect about the y-axis.
7. Stretch vertically by a factor of 8.
8. Shrink vertically by a factor of 8

 

23  The graph of 

$y=f\left(x\right)$

is given

Match each of the following equations with its graph.

1. y = f(x − 4)
2. y = f(x) + 3

C.

$y=\frac{1}{3}f\left(x\right)$

D. y = −f(x + 4)

E. y = 2f(x + 6)