Final Exam

 

1. In​ 2003, an organization surveyed 1,508 adult Americans and asked about a certain​ war, “Do you believe the United States made the right or wrong decision to use military​ force?” Of the 1,508 adult Americans​ surveyed, 1090 stated the United States made the right decision. In​ 2008, the organization asked the same question of 1,508 adult Americans and found that 573 believed the United States made the right decision. Construct and interpret a​ 90% confidence interval for the difference between the two population​ proportions,

$p_{2003}–p_{2008}$

.

The lower bound of a​ 90% confidence interval is ______ ​(Round to three decimal places as​ needed.)

The upper bound of a​ 90% confidence interval is _______ ​(Round to three decimal places as​ needed.)

Interpret the​ 90% confidence interval for the difference between the two population​ proportions,

$p_{2003–2008}.$

. Choose the correct answer below.

1. There is​ 10% confidence that the difference in the proportion of adult Americans from 2003 to 2008 who believe the United States made the right decision to use military force in the country is between the lower and upper bounds of the interval.
2. There is​ 90% confidence that the difference in the proportion of adult Americans from 2003 to 2008 who believe the United States made the right decision to use military force in the country is between the lower and upper bounds of the interval.
3. There is​ 90% confidence that the difference in the proportion of adult Americans from 2003 to 2008 who believe the United States made the right decision to use military force in the country is greater than the lower bound.

 

2.  Classify the variable as qualitative or quantitative.
the native languages of students in an English class

1. qualitative
2. quantitative 

 

3.  The lengths of a particular​ animal’s pregnancies are approximately normally​ distributed, with mean

$\mu = 275$

days and standard deviation 

$\sigma = 12$

days.
​(a) What proportion of pregnancies lasts more than 281  ​days?
​(b) What proportion of pregnancies lasts between 272 and  284 ​days?
​(c) What is the probability that a randomly selected pregnancy lasts no more than 251  ​days?
​(d) A​ “very preterm” baby is one whose gestation period is less than 245 days. Are very preterm babies​ unusual?

​(a) The proportion of pregnancies that last more than 281 days is  _____. ​(Round to four decimal places as​ needed.)
​(b) The proportion of pregnancies that last between 272  and  284 days is ______. (Round to four decimal places as​ needed.)
​(c) The probability that a randomly selected pregnancy lasts no more than 251 days is ______. (Round to four decimal places as​ needed.)
​(d) A​ “very preterm” baby is one whose gestation period is less than 245 days. Are very preterm babies​ unusual?
The probability of this event is _______ so it ______  be unusual because the probability is _______  than 0.05.  (Round to four decimal places as​ needed.)

 

4. Explain what ​90​% ​confidence” means in a 90​% confidence interval.
What does 90​% ​confidence” mean in a 90​% confidence​ interval?

1. The value of the parameter lies within 90 ​% of a standard deviation of the estimate.
2. The probability that the value of the parameter lies between the lower and upper bounds of the interval is 90​%. The probability that it does not is 10​%.
3. If 100 different confidence intervals are​ constructed, each based on a different sample of size n from the same​ population, then we expect 90  of the intervals to include the parameter and 10  to not include the parameter.
4. The confidence interval includes ​90% of all possible values for the parameter.

 

5.  The February utility bills​ (in dollars) for ten residents of a large city are listed below. Find the mode amount.
 71    67     67    72     76    72    73    68     72    72

1. ​$72
2. ​$67
3. ​$76 
4. $73

 

6.   Which branch of statistics deals with the organization and summarization of collected​ information?

1. Survey design
2. Computational statistics
3. Descriptive statistics
4. Inferential statistics

 

7.   The weights​ (in pounds) of babies born at a certain hospital last month are summarized in the table. Find the class width.
 

1. 1 l
2. 1.1 lb
3. 1.05 lb
4. 1.15  lb

 

8.  What is a Type II​ error?

1. An error that fails to reject
   $H_0$

   ​, given that

   $H_1$

    is true. 

2. An error that fails to reject
   $H_0$

   ​, given that  

   $H_1$

   is false.

3. An error that rejects 
   $H_0$

   ​, given that 

   $H_1$

   is true.

4. An error that rejects 
   $H_0$

   ​, given that 

   $H_1$

     is false.

 

9.  Fill in the blanks to complete the statement.
The​ _______ _______ is a statement we are trying to find evidence to support.

 

10.  Classify the variable as qualitative or quantitative.
the temperatures of cups of coffee served at a restaurant

1. qualitative
2. quantitative 

 

11.  SAS was used to compare the high school dropout rates for the 30 school districts in one city in 2010 and 2012. The boxplots generated for these dropout rates are

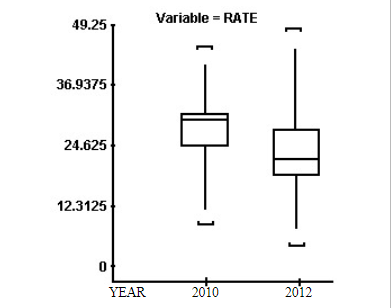
1. Dropout rates had a higher average with less variability in 2010 than in 2012. 
2. Dropout rates had a lower average with more variability in 2010 than in 2012.
3. Dropout rates had a higher average with more variability in 2010 than in 2012.
4. Dropout rates had a lower average with less variability in 2010 than in 2012.

 

12. The grades are given for a student for a particular term. Find the grade point average. An A is worth 4​ points, a B is worth 3​ points, a C is worth 2​ points, a D is worth 1​ point, and an F is worth 0 points.

     

 

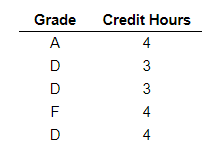
1. 0.37
2. 1.44
3. 1.40
4. 3.60

 

 

13.  A stock analyst wondered whether the mean rate of return of​ financial, energy, and utility stocks differed over the past 5 years. He obtained a simple random sample of eight companies from each of the three sectors and obtained the​ 5-year rates of return shown in the accompanying table​ (in percent). Complete parts​ (a) through​ (d) below.

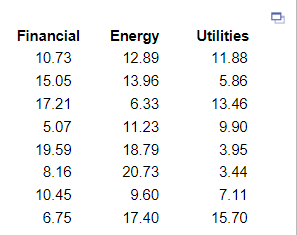
(a) State the null and alternative hypotheses. Choose the correct answer below.
​

(b) Normal probability plots indicate that the sample data come from normal populations. Are the requirements to use the​ one-way ANOVA procedure​ satisfied?

1. ​No, because there are k=3 simple random​ samples, one from each of k​ populations, the k samples are independent of each​ other, and the populations are normally distributed and have the same variance. 
2. ​Yes, because there are k=3 simple random​ samples, one from each of k​ populations, the k samples are independent of each​ other, and the populations are normally distributed and have the same variance. 
3. ​No, because the largest sample standard deviation is more than twice the smallest sample standard deviation.
4. ​Yes, because there are k=3 simple random​ samples, one from each of k​ populations, the k samples are independent of each​ other, and the populations are normally distributed and have different variances.

 

(c) Are the mean rates of return different at the

$\alpha$

= 0.05 level of​ significance?

Use technology to find the​ F-test statistic for this data set.

$F_{0 } =$

_____ ​(Round to two decimal places as​ needed.)

Determine the​ P-value and state the appropriate conclusion below.

Since the​ P-value is _______, there ________ enough evidence to reject the null hypothesis.​ Thus, we ______  conclude that the mean rates of return are different at the

$\alpha =$

0.05 level of significance.

 

14.  A player is dealt one card from a 52 card deck. Then the card is replaced in the​ deck, the deck is​ shuffled, and the player draws again. Find the probability of the player getting a picture card the first time and a heart  the second time. Express the probability as a simplified fraction.

1. $\frac{3}{13}$
2. $\frac{1}{4}$
3. $\frac{3}{52}$
4. $\frac{1}{13}$

 

 

15.   In the probability distribution to the​ right, the random variable X represents the number of marriages an individual aged 15 years or older has been involved in. Complete parts​ (a) through​ (f) below.

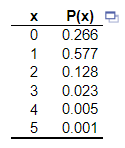
​(a) Verify that this is a discrete probability distribution.

This is a discrete probability distribution because ______________  between  _____ and  ____​, ​inclusive, and the _____ of the probabilities is ____.  ​(Type whole numbers. Use ascending​ order.)
​

(b) Draw a graph of the probability distribution. Describe the shape of the distribution.

Describe the shape of the distribution.

The distribution __________  and is  __________

​(c) Compute and interpret the mean of the random variable X.

${\mu }_x =$

______ marriages.  ​(Type an integer or a decimal. Do not​ round.)

Which of the following interpretations of the mean is​ correct?

1. If any number of individuals aged 15 year or older were​ surveyed, one would expect the mean number of marriages to be the mean of the random variable.
2. The observed number of marriages will be less than the mean number of marriages for most individuals.
3. The observed number of marriages will be equal to the mean number of marriages for most individuals.
4. If many individuals aged 15 year or older were​ surveyed, one would expect the mean number of marriages to be the mean of the random variable.

 

16.  Suppose a basketball player is an excellent free throw shooter and makes 94​% of his free throws​ (i.e., he has a 94​% chance of making a single free​ throw). Assume that free throw shots are independent of one another. Suppose this player gets to shoot three free throws. Find the probability that he misses all three  consecutive free throws. Round to the nearest​ ten-thousandth.

1. 0.9998
2. 0.8306
3. 0.0002
4. 0.1694

 

 

17.   Two researchers conducted a study in which two groups of students were asked to answer 42  trivia questions from a board game. The students in group 1 were asked to spend 5 minutes thinking about what it would mean to be a​ professor, while the students in group 2 were asked to think about soccer hooligans. These pretest thoughts are a form of priming. The 200 students in group 1 had a mean score of 23.9 with a standard deviation of 3.7​, while the 20 students in group 2 had a mean score of 15.2  with a standard deviation of 3.2. Complete parts ​(a) and ​(b) below.

​(a) Determine the 95​% confidence interval for the difference in​ scores, 

${\mu }_1–{\mu }_2$

. Interpret the interval.
The lower bound is _____ .

The upper bound is _____.  ​(Round to three decimal places as​ needed.)

Interpret the interval. Choose the correct answer below. 

1. There is a 95​% probability that the difference of the means is in the interval. 
2. The researchers are 95​% confident that the difference of the means is in the interval. 
3. The researchers are 95​% confident that the difference between randomly selected individuals will be in the interval. 
4. There is a 95​% probability that the difference between randomly selected individuals will be in the interval.

 

(b) What does this say about​ priming?

1. Since the 95​% confidence interval does not contain​ zero, the results suggest that priming does have an effect on scores. 
2. Since the 95​% confidence interval contains​ zero, the results suggest that priming does have an effect on scores.
3. Since the 95​% confidence interval contains​ zero, the results suggest that priming does not have an effect on scores.
4. Since the 95​% confidence interval does not contain​ zero, the results suggest that priming does not have an effect on scores.

 

18.   Classify the variable as qualitative or quantitative.
the number of seats in a school auditorium

1. quantitative 
2. qualitative 

 

19.   The level of​ significance, 

$\alpha$

​, is the probability of making​ what?

1. A type
   $\beta$

   error

2. A correct decision
3. Atype I error
4. A type II error

 

20.  The sample space for tossing three fair coins is​ {HHH, HHT,​ HTH, HTT,​ THH, THT,​ TTH, TTT}. What is the probability of exactly two​ heads?

1. 3
2. $\frac{1}{2}$
3. $\frac{5}{8}$
4. $\frac{3}{8}$

 

 

21.  If the null hypothesis is rejected when the null hypothesis is​ true, what type of​ error, if​ any, has been​ made?

1. Type
   $\alpha$

   error

2. Type I error
3. Type II error
4. Correct decision

 

 

22.  Which of the following is not true of​ statistics?

1. Statistics involves collecting and summarizing data.  
2. Statistics can be used to organize and analyze information.
3. Statistics is used to draw conclusions using data. 
4. Statistics is used to answer questions with​ 100% certainty.

 

 

23.  The following Venn diagram is for the six sample points possible when rolling a fair​ 6-sided die. Let A be the event rolling an even number and let B be the event rolling a number greater than 1. Which of the following events describes the event rolling a​ 1?

1. $A^c$
2. B
3. $B^c$
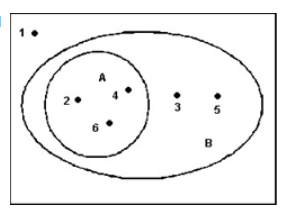
4. $A \cup B$

 

24.  Describe the shape of the distribution.

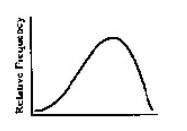
1. The distribution is skewed to the left.
2. B.The distribution is bell shaped.
3. The distribution is skewed to the right.
4. The distribution is uniform.

 

25.  Find the value of

$Z_{\alpha }$

.

$Z_{0.46}$

=

 

26.  The time required for an automotive center to complete an oil change service on an automobile approximately follows a normal​ distribution, with a mean of 17  minutes and a standard deviation of 2.5 minutes.
​(a) The automotive center guarantees customers that the service will take no longer than 20  minutes. If it does take​ longer, the customer will receive the service for​ half-price. What percent of customers receive the service for​ half-price?
​(b) If the automotive center does not want to give the discount to more than ​3% of its​ customers, how long should it make the guaranteed time​ limit?

 

27.  A golf association requires that golf balls have a diameter that is 1.68 inches. To determine if golf balls conform to the​ standard, a random sample of golf balls was selected. Their diameters are shown in the accompanying data table. Do the golf balls conform to the​ standards? Use the  

$\alpha = 0.05$

level of significance.

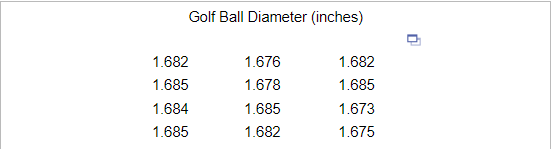
First determine the appropriate hypotheses.

$$\begin{gathered} H_{0:}: \\ {H}_1: \end{gathered}$$

Find the test statistic.  _____  ​(Round to two decimal places as​ needed.)

Find the​ P-value. _____ (Round to three decimal places as​ needed.)

What can be concluded from the hypothesis​ test?

1. Do not reject
   $H_0$

   . There is sufficient evidence to conclude that the golf balls do not conform to the​ association’s standards at the

   $\alpha =0.05$

    level of significance.

2. Do not reject
   $H_0$

   . There is not sufficient evidence to conclude that the golf balls do not conform to the​ association’s standards at the

   $\alpha = 0.05$

    level of significance.

3. Reject
   $H_0$

   . There is not sufficient evidence to conclude that the golf balls do not conform to the​ association’s standards at the

   $\alpha = 0.05$

    level of significance.

4. Reject
   $H_0$

   . There is sufficient evidence to conclude that the golf balls do not conform to the​ association’s standards at the 

   $\alpha = 0.05$

     level of significance.