Section 5.4 Homework

1.  The notation P(F E) means the probability of event _____  given event _____

2. Suppose that E and F are two events and that P(E and F)=0.1 and P(E)=0.2.

What is P(F|E)​?_____________ ​(Type an integer or a​ decimal.)

3.  Suppose that E and F are two events and that N(E and F)=240 and N(E)=470.

What is P(F|E)​? ______ (Round to three decimal places as​ needed.)

4.  Suppose that E and F are two events and that P(E)=0.2 and P(F|E)=0.9.

What is P(E and F)​? ____________

5.  The probability that a randomly selected individual in a country earns more than​ $75,000 per year is 8.5​%. The probability that a randomly selected individual in the country earns more than​ $75,000 per​ year, given that the individual has earned a​ bachelor’s degree, is 8.5​%.  Are the events​ “earn more than​ $75,000 per​ year” and​ “earned a​ bachelor’s degree”​ independent?

Are these events​ independent?

1. Yes
2. No

6.  In a recent​ poll, a random sample of adults in some country​ (18 years and​ older) was​ asked, “When you see an ad emphasizing that a product is​ “Made in our​ country,” are you more likely to buy​ it, less likely to buy​ it, or neither more nor less likely to buy​ it?” The results of the​ survey, by age​ group, are presented in the following contingency table. Complete parts​ (a) through​ (c).

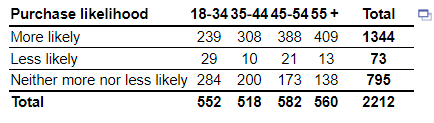
(a) What is the probability that a randomly selected individual is at least 55 years of​ age, given the individual is more likely to buy a product emphasized as​ “Made in our​ country”?

The probability is approximately ______   (Round to three decimal places as​ needed.)

​(b) What is the probability that a randomly selected individual is more likely to buy a product emphasized as​ “Made in our​ country,” given the individual is at least 55 years of​ age?

The probability is approximately _______  (Round to three decimal places as​ needed.)

​(c) Are​ 18- to​ 34-year-olds more likely to buy a product emphasized as​ “Made in our​ country” than individuals in​ general?

1. ​Yes, more likely
2. ​No, less likely

7.  Suppose you just received a shipment of fourteen televisions. Four of the televisions are defective. If two televisions are randomly​ selected, compute the probability that both televisions work. What is the probability at least one of the two televisions does not​ work?

The probability that both televisions work is _______  (Round to three decimal places as​ needed.)

The probability that at least one of the two televisions does not work is _____   (Round to three decimal places as​ needed.)

8.  Suppose you just purchased a digital music player and have put 10 tracks on it. After listening to them you decide that you like 4 of the songs. With the random feature on your​ player, each of the 10 songs is played once in random order. Find the probability that among the first two songs played

​(a) You like both of them. Would this be​ unusual?

​(b) You like neither of them.

​(c) You like exactly one of them.

​(d) Redo​ (a)-(c) if a song can be replayed before all 10 songs are played.

​

(a) The probablility that you like both songs is ______  (Round to three decimal places as​ needed.)

Would it be unusual for you to like both of the​ songs?

1. Yes
2. No

​(b) The probability that you like neither song is ______ ​(Round to three decimal places as​ needed.)

​(c) The probability that you like exactly one song is _____  (Round to three decimal places as​ needed.)

​(d) The probability that you like both songs is _______  (Round to three decimal places as​ needed.)

The probability that you like neither song is ________  (Round to three decimal places as​ needed.)

The probability that you like exactly one song is _______  (Round to three decimal places as​ needed.)

9.   Suppose there is a 24.5% probability that a randomly selected person aged 30 years or older is a smoker. In​ addition, there is a 11.6% probability that a randomly selected person aged 30 years or older is female, given that he or she smokes. What is the probability that a randomly selected person aged 30 years or older is female and smokes?

Would it be unusual to randomly select a person aged 30 years or older who is female and smokes?The probability that a randomly selected person aged 30 years or older is female and smokes is ______  (Round to three decimal places as​ needed.).

Would it be​ unusual?

1. Yes
2. No

10   The following data represent the number of different communication activities used by a random sample of teenagers in a given week. Complete parts​ (a) through​ (d).

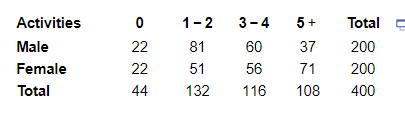
​(a) Are the events ​”male​” and ​”0 ​activities” independent?

 ​(b) Are the events ​”female​” and ​”5+ ​activities” independent?

 ​(c) Are the events ​”1−2 ​activities” and ​”5+ ​activities” mutually​ exclusive?

 ​(d) Are the events ​”male​” and ​”1−2 ​activities” mutually​ exclusive?

11.  Suppose that a computer chip company has just shipped 10,000 computer chips to a computer company.​ Unfortunately, 60 of the chips are defective.

​(a) Compute the probability that two randomly selected chips are defective using conditional probability.

​(b) The probability that the first randomly selected chip is defective is

=0.006=0.6%.

Compute the probability that two randomly selected chips are defective under the assumption of independent events.

​(a) The probability is ______  (Round to eight decimal places as​ needed.)

​(b) The probability is ________  (Round to eight decimal places as​ needed.)

When small samples are taken from large populations without​ replacement, the assumption of independence does not significantly affect the probability. Based on the​ results, what does this​ mean?

1. The probabilities are nearly the same.
2. The probabilities are exactly the same.
3. The probabilities are very​ different, but the probability found assuming independent events is​ larger, so it does not matter.
4. The probabilities are very​ different, but the probability found assuming independent events is​ smaller, so it does not matter.