Navigation » List of Schools, Subjects, and Courses » Math 138 – Statistics » Homeworks » 5.2 Homework
No Answers We dont have answer to this question yet. If you need help with your homework send us an email  or chat with our tutors
or chat with our tutors
5.2 Homework
5.2 Homework
1. Fill in each blank with the appropriate word or phrase.
If events A and B are mutually exclusive, then P (A or B) = ________.
The General Addition Rule states that P (A or B) = P (A) + P (B) – ______________.
2. If P (A) = 0.5, P (B) = 0.6, and P (A and B) = 0.42, find P (A or B).
P (A or B) =
3. If P (A) = 0.5, P (B) = 0.1, and A and B are mutually exclusive, find P ( A or B).
P (A or B) =
4. Determine whether events A and B are mutually exclusive. A sample of 30 books is selected from the library.
A: At least 10 of the books are mysteries.
B: At least 10 of the authors are male.
These events _______ mutually exclusvie
5. If
= 0.1 , find P (B).
P (B) =
6. A sample of 100 internet users was selected. Find the complements of the following events.
(a)More than 70 of them use Google as their primary search engine.
The complement is:
_____ of them use Google as their primary search engine.
(b)At least of 70 them use Google as their primary search engine.
The complement is:
________ of them use Google as their primary search engine.
(c)Fewer than 70 of them use Google as their primary search engine.
The complement is:
_______ of them use Google as their primary search engine.
(d) Exactly 70 of them use Google as their primary search engine.
The complement is:
The number of internet users using Google as their primary search engine is _________.
7. Car repairs: Let E be the event that a new car requires engine work under warranty and let T be the event that the car requires transmission work under warranty. Suppose that P (E) = 0.04, P (T) = 0.09, P (E and T) = 0.02.
(a) Find the probability that the car needs work on either the engine, the transmission, or both.
(b) Find the probability that the car needs no work on the transmission.
(a) Find the probability that the car needs work on either the engine, the transmission, or both.
The probability that the car needs work on either the engine, the transmission, or both is ______ .
(b) Find the probability that the car needs no work on the transmission.
The probability that the car needs no work on the transmission is _______.
8. Weight and cholesterol: The National Health Examination Survey reported that in a sample of 13,101 adults, 6157 had high cholesterol (total cholesterol above 200 ml/dL), 8778 were overweight (body mass index above 25 ), and 4192 were both overweight and had high cholesterol. A person is chosen at random from this study. Round all answers to four decimal places.
(a)Find the probability that the person is overweight.
The probability that the person is overweight is ________ .
(b)Find the probability that the person has high cholesterol.
The probability that the person has high cholesterol is ______ .
(c)Find the probability that the person does not have high cholesterol.
The probability that the person does not have high cholesterol is _______ .
(d)Find the probability that the person is overweight or has high cholesterol.
The probability that the person is overweight or has high cholesterol is _____ .
9. The following table presents the number of reports of graffiti in each of New York’s five boroughs over a one-year period. These reports were classified as being open, closed, or pending. A graffiti report is selected at random. Compute the following probabilities. Round final answer to four decimal places.
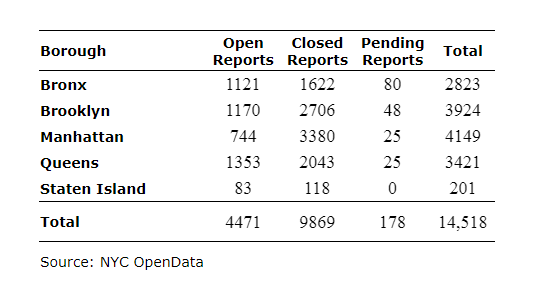
(a) The report is open and comes from Staten Island.
The probability that the report is open and comes from Staten Island is ____ .
(b) The report is closed or comes from Bronx.
The probability that the report is closed or comes from Bronx is _____ .
(c) The report comes from Brooklyn.
The probability that the report comes from Brooklyn is _____.
(d) The report that does not come from Brooklyn.
The probability that the report does not come from Brooklyn is ______ .
(e) The report is open.
The probability that the report is open is _____.
(f) The report is from the Brooklyn or Queens.
The probability that the report is from the Brooklyn or Queens is _____.
10. According to the National Health Statistics Reports, 16% of American women have one child, and 21% have two children. Is the probability that a woman has either one or two children equal to 0.16 + 0.21 = 0.37?
The probability that a woman has either one or two children ____ equal to 0.16 _ 0.21 = 0.37 because the two events ____ mutually exclusive.
 or chat with our tutors
or chat with our tutors
