Test 1

Navigation » List of Schools, Subjects, and Courses » Math 266 – Calculus Analytical Geometry 2 » Tests » Test 1

With Answers Good news! We are showing you only an excerpt of our suggested answer to this question. Should you need our help in customizing an answer to this question, feel free to send us an email at or chat with our customer service representative.

Question

Test 1

Find the antiderivative

\int e^{2 - 3 x} d x

\int_{1}^{\sqrt{3}} x e^{x^{2}} d x

\int_{\ln 2}^{\ln (2 / \sqrt{3})} \frac{e^{- x}}{\sqrt{1 - e^{- 2 x}}} d x

\int \ln x / x d x

5. A. Find the area enclosed by y = 5x –

x^{2}

and y = x. Solve and Draw.

B. Set up the integral for the area enclosed by y = 5x –

x^{2}

and y = x from x = –2 to 6. Do not solve.

7. Draw and set up the integrals for the area enclosed by x = 2

y^{2}

and y = 2x,

A. as type I region

B. as type II region

8. Draw and set up the integrals for the area enclosed by y = 4x –

x^{2}

and y =

x^{2}

: A. as type I region B. as type II region

9. (Do not solve) Set up the integrals for the volumes of solids of revolution by revolving the following triangular templates about the given axes using the washer method. Draw and show the formulas for the radii R and r. clearly A. x = –10, B. y=10

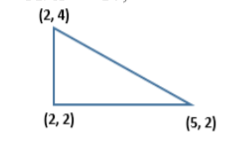
10. A and B. (Do not solve) Set up the integrals for the volumes of solids of revolution by revolving in problem 9 using cylindrical shell method. Draw and show the formulas for the radius r and the height h clearly.

Need help with your discussion preparation?

Existing Clients Login here

View Our Sample Answer

This question is taken from Math 266 – Calculus Analytical Geometry 2 » Fall 2021 » Tests

View All Questions