Section 2.2 Homework

1.  Find the derivative of the function using the definition of derivative.

$g\left(x\right) = \sqrt{1–x}$

g'(x) = _____________

State the domain of the function. (Enter your answer using interval notation.)

State the domain of its derivative. (Enter your answer using interval notation.)

2.  Find the derivative of the function using the definition of derivative.

$g\left(t\right)=\frac{3}{\sqrt{t}}$

$g‘\left(5\right)=$

State the domain of the function. (Enter your answer using interval notation.)

State the domain of its derivative. (Enter your answer using interval notation.)

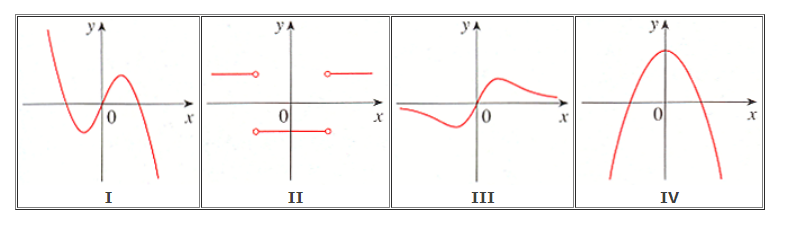
3.   The graphs of four derivatives are given below. Match the graph of each function in (a)-(d) with the graph of its derivative in I-IV.

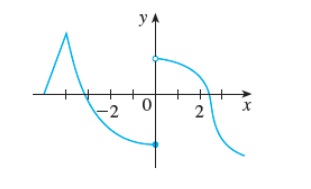
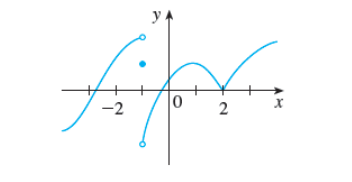
4. The graph of f is given. State the numbers at which f is not differentiable.
x    =        (smaller value)
x    =        (larger value)

5. Find the derivative of the function using the definition of derivative.

$f\left(t\right) = 7t–4t^2$

f’t= ___________

State the domain of the function. (Enter your answer using interval notation.)

State the domain of its derivative. (Enter your answer using interval notation.)

6.   The graph of f is given. State the numbers at which f is not differentiable.
x    =       (smaller value)
x    =       (larger value)

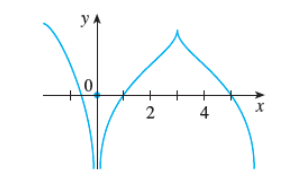
7.   The graph of f is given. State the numbers at which f is not differentiable.
x    =      (smaller value)
x    =      (larger value)

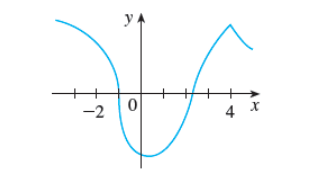
8.  The graph of f is given. State the numbers at which f is not differentiable.
x    =     (smaller value)
x    =     (larger value)

Section 2.2 Homework Answers

4. The graph of f is given. State the numbers at which f is not differentiable.

Answer:

x    =   -4     (smaller value)
x    =      0  (larger value)