Chapter 1.1 Homework

1. The graph of a function f is given in the figure.

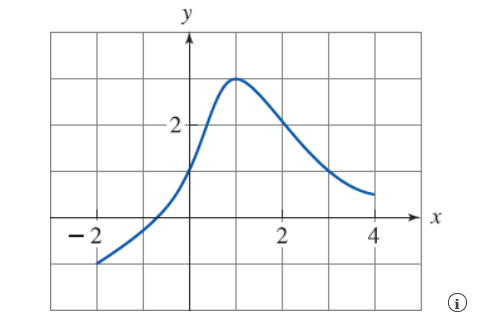
The graph of a function f is given in the figure.

(a) Find the value of f(1).

(b) Estimate the value of f(−1).

(c) For what values of x is f(x) = 1?  (Enter your answers as a comma-separated list.)

(d) Estimate the value of x such that f(x) = 0.

(e) State the domain and range of f. (Enter your answers in interval notation.) domain ____, range ____

(f) On what interval is f increasing? (Enter your answer using interval notation.)

 

2. The graphs of f and g are given in the figure.

(a) State the values of f(0) and g(−2).

(b)Which is larger, f(−4) or g(−4)?

(c) For what values of x is f(x) = g(x)?  (Enter your answers as a comma-separated list.)

x = 

(d) On what interval(s) is f(x) ≤ g(x)?  (Enter your answer using interval notation.)

(e) State the solution of the equation f(x) = −1.  (Enter your answers as a comma-separated list.)

x = 

(f) On what interval(s) is g decreasing? (Enter your answer using interval notation.)

(g) State the domain and range of f. (Enter your answers using interval notation.)

domain

range

(h) State the domain and range of g. (Enter your answers using interval notation.)

domain

range

 

3.  Consider the following graph.

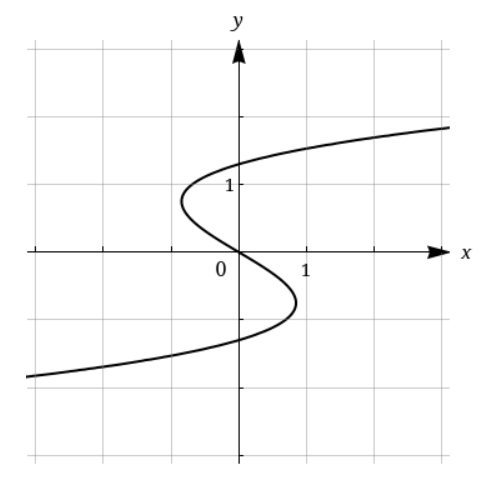
Determine whether the curve is the graph of a function of x.

Yes, it is a function

No, it is not a function

 

If it is, state the domain and range of the function. (Enter your answers using interval notation. If it is not a function, enter NAF in all blanks.)

Domain

Range

 

4.  Consider the following graph.

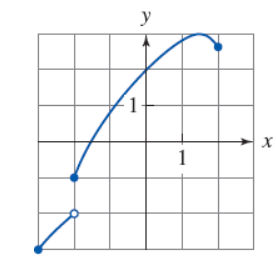
Determine whether the curve is the graph of a function of x.

Yes, it is a function

No, it is not a function

 

If it is, state the domain and range of the function. (Enter your answers using interval notation. If it is not a function, enter NAF in all blanks.)

Domain

Range

 

5. Evaluate the difference quotient for the given function. Simplify your answer.

$f\left(x\right)=3+5x–x^2, \frac{f\left(3+h\right)–f\left(3\right)}{h}$

 

6. Evaluate the difference quotient for the given function. Simplify your answer.

$f\left(x\right)=\frac{x+8}{x+2}, \frac{f\left(x\right)–f\left(4\right)}{x–4}$

 

7.  Find the domain of the function. (Enter your answer using interval notation.)

$f\left(x\right)=\frac{x+4}{x^2–4}$

 

8.   Find the domain of the function. (Enter your answer using interval notation.)

$f\left(t\right)=\sqrt[3]{8t–5}$

 

9.  Find the domain and range of the function. (Enter your answers using interval notation.)

h

$h\left(x\right)=\sqrt{4–x^2}$

Domain

Range

 

10. Evaluate f(−9), f(0), and f(8) for the piecewise defined function.

$f\left(x\right)=\left\{\begin{array}{l}x+2 if x < 0\\ 1–x if x \ge 0\end{array}\right.$

$$\begin{gathered} f\left(–9\right) = \\ f\left(0\right) = \\ f \left(8\right) = \end{gathered}$$

 

11.  Sketch the graph of the function.

$f\left(x\right) = x + \left|x\right|$

 

12.  Sketch the graph of the function.

$f\left(x\right) = \left\{\begin{array}{l}5\left|x\right| if \left|x\right| \le 1\\ 5 if \left|x\right| \ge 1\end{array}\right.$

 

13.  Find a formula for the function whose graph is the given curve.

the bottom half of the parabola

$x + {\left(y–9\right)}^2=0$

 

14.   Find a formula for the function whose graph is the given curve.

the top half of the circle

$x^2+ {\left(y–1\right)}^2=9$

 

15.  Find a formula for the described function.  A rectangle has perimeter 12 m. Express the area A (in m²) of the rectangle as a function of the length, L, of one of its sides.

A(L) = ___

$m^2$

State the domain of A. (Assume the length of the rectangle is longer than its width. Enter your answer using interval notation.)

 

16.  Find a formula for the described function. Express the area A of an equilateral triangle as a function of the length of a side x.

A(x) =

$\frac{\sqrt{3}}{4}{x}^2$

 

17.  Graphs of f and g are shown.

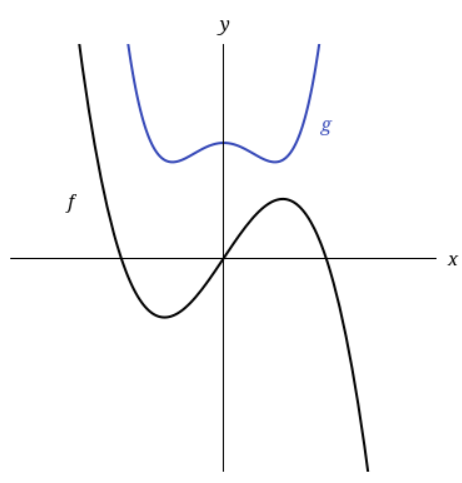
Is f even, odd, or neither?

1. even
2. odd
3. neither

 

Explain your reasoning.

1. It is symmetric about the origin
2. It is symmetric with respect to the y-axis
3. It is symmetric with respect to the x-axis
4. It is not symmetric about the origin or the y-axis

 

Is g even, odd, or neither?

1. Even
2. Odd
3. Neither

 

Explain your reasoning.

1. It is symmetric about the origin.
2. It is symmetric with respect to the y-axis.    
3. It is symmetric with respect to the x-axis.
4. It is not symmetric about the origin or the y-axis.

 

18.  If the point (6, 9) is on the graph of an even function, what other point must also be on the graph?

If the point (6, 9) is on the graph of an odd function, what other point must also be on the graph?

 

19.  A graphing calculator is recommended.

Determine whether f is even, odd, or neither. Use technology to check your answer visually.

$f\left(x\right) = \frac{x}{x^2+9}$

1. Even
2. Odd
3. Neither

 

20.   A graphing calculator is recommended.

Determine whether f is even, odd, or neither. Use technology to check your answer visually.

f(x) = x|x|

1. Even
2. Odd
3. Neither

 

21 Find the domain of the function. (Enter your answer using interval notation.)

$f\left(t\right) = \sqrt{t} + \sqrt[3]{t}$

 

22. Find the domain of the function. (Enter your answer using interval notation.)

$g\left(u\right) = \sqrt{u} + \sqrt{2–u}$

 

23.   Find the domain of the function. (Enter your answer using interval notation.)

$H\left(t\right) = \frac{4 – t^2}{2 – t}$

 

24.   Find the domain of the function. (Enter your answer in interval notation.)

$g\left(x\right) = \sqrt{x–19}$

 

25.  Use the Vertical Line Test to determine whether the curve is the graph of a function x. State the domain and range of the function. (If the curve is not a function, choose NONE.)

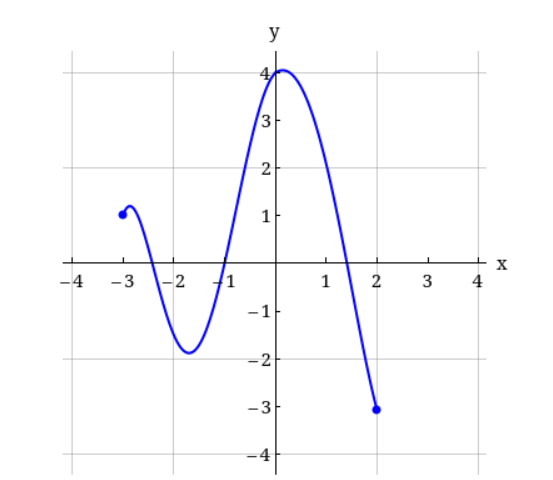
1. The given curve is the graph of a function of x, by the Vertical Line Test.
2. The given curve is not the graph of a function of x, by the Vertical Line Test.  

 

26. Find the domain of the function.

$g\left(x\right) = \sqrt{x^2–36}$

 

27.  Find the domain of the function.

$f\left(x\right) =\frac{x}{\sqrt[4]{9–x^2}}$

 

28.  Consider the rational function f given below.

$f\left(x\right) = \frac{x}{x^2+4x–21}$