Navigation » List of Schools, Subjects, and Courses » Math 190 – Calculus with Analytic Geometry » Homeworks » Chapter 1.4 Homework
No Answers We dont have answer to this question yet. If you need help with your homework send us an email  or chat with our tutors
or chat with our tutors
Chapter 1.4 Homework
Chapter 1.4 Homework
1. The point P(8, −2) lies on the curve
A. If Q is the point
find the slope of the secant line PQ (correct to six decimal places) for the following values of x.
B Using the results of part (a), guess the value of the slope of the tangent line to the curve at P(8, −2). m=
C. Using the slope from part (b), find an equation of the tangent line to the curve at
P(8, −2).
2 A graphing calculator is recommended.
If a ball is thrown into the air with an initial velocity of 44 ft/s, its height in feet after t seconds is given by y = 44t − 16t2.
(a) Find the average velocity of the ball (in ft/s) for the time interval beginning at t = 2 and lasting for each of the following.
- 0.5 seconds
- 0.1 seconds
- 0.05 seconds
- 0.01 seconds
b. Use your answers from part (a) to estimate the instantaneous velocity (in ft/s) when t = 2.
3. A graphing calculator is recommended.
The displacement (in centimeters) of a particle s moving back and forth along a straight line is given by the equation s = 3 sin(𝜋t) + 3 cos(𝜋t), where t is measured in seconds. (Round your answers to two decimal places.)
A. Find the average velocity during each time period.
- [1,2]
- [1,1.1]
- [1,1.01]
- [1,1.001]
B. Estimate the instantaneous velocity of the particle when t = 1.
4. The point P(6, 1) lies on the curve
(a) If Q is the point
use your calculator to find the slope of the secant line PQ (correct to six decimal places) for the following values of x.
(b) Using the results of part (a), guess the value of the slope of the tangent line to the curve at P(6, 1).
(c) Using the slope from part (b), find an equation of the tangent line to the curve at P(6, 1).
(d) Sketch the curve, two of the secant lines, and the tangent line.
5. Find the slope of the line through P and Q.
P(0, 0), Q(4, 2)
6. Find the slope of the line through P and Q.
P(5, −5), Q(−1, 2)
7. Make a table of values for the equation. y = x2 − 1
8. Make a table of values for the equation. y = x2 − 1
9. Find the x– and y-intercepts. (If an answer does not exist, enter DNE.)
x intercept
y intercept
10. A tank holds 3,000 gallons of water, which drains from the bottom of the tank in half an hour. The values in the table show the volume V of water remaining in the tank (in gallons) after t minutes.
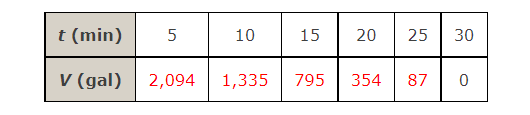
If P is the point (15, 795) on the graph of V, find the slopes of the secant lines PQ when Q is the point on the graph with t = 5, 10, 20, 25, and 30. (Round your answers to one decimal place.)
| Q | Slope |
| (5, 2,094) | |
| (10, 1,335) | |
| (20, 354) | |
| (25, 87) | |
| (30, 0) |
Estimate the slope of the tangent line at P by averaging the slopes of the two adjacent secant lines corresponding to the two points closest to P. (Round your answer to one decimal place.)
11. Consider the following function.
(a) Find an equation of the tangent line to the graph of f at the given point.
(b) Use a graphing utility to graph the function and its tangent line at the point.
12. Consider the following function.
(a) Find an equation of the tangent line to the graph of f at the given point.
(b) Use a graphing utility to graph the function and its tangent line at the point.
13. A cardiac monitor is used to measure the heart rate of a patient after surgery. It compiles the number of heartbeats after t minutes. When data in the table are graphed, the slope of the tangent line represents the heart rate in beats per minute.
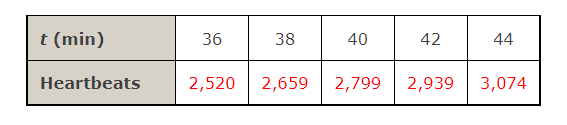
The monitor estimates this value by calculating the slope of a secant line. Use the data to estimate the patient’s heart rate after 42 minutes using the secant line between the points with the given values of t. (Round your answers to one decimal place.)
A. t=36 and t=42
B. t=38 and t=42
C. t=40 and t=42
D. t=42 and 5=44
 or chat with our tutors
or chat with our tutors
