Quiz 5

1.  A concrete mix is designed to withstand 3000 pounds per square inch​ (psi) of pressure. The following data represent the strength of nine randomly selected casts​ (in psi).

3950​, 4080​, 3300​, 3100​, 2930​, 3820​, 4080​, 4030​, 3470

  Compute the mode strength of the concrete. Select the correct choice below​ and, if​ necessary, fill in the answer box to complete your choice.

1. The mode of the strengths of the concrete is ____ psi of pressure.  ​(Round to the nearest tenth as​ needed.)
2. The mode does not exist.

2.   Find the population mean or sample mean as indicated.

​Population: 2​, 8​, 10​, 16​, 24

Select the correct choice below and fill in the answer box to complete your choice.

3.    The following data represent the monthly cell phone bill for a​ person’s phone for six randomly selected months.

​$35.40​, ​$42.09​, ​$39.47​, ​$38.93​, ​$43.39​, ​$49.26

Compute the median phone bill.

The median phone bill is ______  (Round to the nearest cent as​ needed.)

4.   The following data represent the amount of time​ (in minutes) a random sample of eight students took to complete the online portion of an exam in a particular statistics course. Compute the​ mean, median, and mode time.

67.4​, 80.6​, 88.9​, 114.7​, 128.4​, 102.2​, 94.7​, 125.7

 Compute the mean exam time. Select the correct choice below​ and, if​ necessary, fill in the answer box to complete your choice.

1. The mean exam time is _____  (Round to two decimal places as​ needed.)
2. The mean does not exist.

Compute the median exam time. Select the correct choice below​ and, if​ necessary, fill in the answer box to complete your choice.

1. The median exam time is _____  (Round to two decimal places as​ needed.)
2. The median does not exist.

Compute the mode exam time. Select the correct choice below​ and, if​ necessary, fill in the answer box to complete your choice.

1. The mode is ____ ​(Round to two decimal places as needed. Use a comma to separate answers as​ needed.)
2. The mode does not exist.

5.  The following data represent exam scores in a statistics class taught using traditional lecture and a class taught using a​ “flipped” classroom. Complete parts​ (a) through​ (c) below.

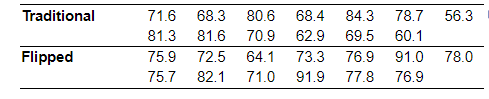
(a) Which course has more dispersion in exam scores using the range as the measure of​ dispersion?

The traditional course has a range of _____ while the​ “flipped” course has a range of

The _____  course has more dispersion.  ​(Type integers or decimals. Do not​ round.)

​

(b) Which course has more dispersion in exam scores using the sample standard deviation as the measure of​ dispersion?

The traditional course has a standard deviation of _____ while the​ “flipped” course has a standard deviation of ______

The _________ course has more dispersion.  ​(Round to three decimal places as​ needed.)

​

(c) Suppose the score of 60.1 in the traditional course was incorrectly recorded as 601.  How does this affect the​ range?

The range is now _____  (Type an integer or a decimal. Do not​ round.)

How does this affect the standard​ deviation?

The standard deviation is now ____  (Round to three decimal places as​ needed.)

What property does this​ illustrate?

1. The standard deviation is​ resistant, but the range is not resistant.
2. Neither the range nor the standard deviation is resistant.
3. Both the range and the standard deviation are resistant.
4. The range is​ resistant, but the standard deviation is not resistant.

6.  A certain standardized​ test’s math scores have a​ bell-shaped distribution with a mean of 520 and a standard deviation of 105.

Complete parts​ (a) through​ (c).

​(a) What percentage of standardized test scores is between 415 and 625​? ___ ​(Round to one decimal place as​ needed.)

​(b) What percentage of standardized test scores is less than 415 or greater than 625​? ____ ​(Round to one decimal place as​ needed.)

​(c) What percentage of standardized test scores is greater than 730​? ____ ​(Round to one decimal place as​ needed.)

7.  In December​ 2018, the average price of regular unleaded gasoline excluding taxes in the United States was ​$3.06 per gallon. Assume that the standard deviation price per gallon is ​$0.07 per gallon and use​ Chebyshev’s Inequality to answer the following.

​(a) What minimum percentage of gasoline stations had prices within 2 standard deviations of the​ mean?

​(b) What minimum percentage of gasoline stations had prices within 2.5 standard deviations of the​ mean? What are the gasoline prices that are within 2.5 standard deviations of the​ mean?

​(c) What is the minimum percentage of gasoline stations that had prices between ​$2.78 and ​$3.34​?

​

(a) At least ____ of gasoline stations had prices within 2 standard deviations of the mean.  ​(Round to two decimal places as​ needed.)

​(b) At least ____ of gasoline stations had prices within 2.5 standard deviations of the mean.  ​(Round to two decimal places as​ needed.)

The gasoline prices that are within 2.5 standard deviations of the mean are  ______  to  _______ ​(Type integers or decimals. Do not round. Use ascending​ order.)

​(c) _______ is the minimum percentage of gasoline stations that had prices between $2.78 and ​$3.34.

​(Round to two decimal places as​ needed.)

8.  Which of the following measures of dispersion is​ resistant, if​ any?  Select all that apply.

1. Range
2. Standard deviation
3. Variance
4. None of these measures of dispersion is resistant.