Section 5.1 Homework

 

1.   What is the probability of an event that is​ impossible? Suppose that a probability is approximated to be zero based on empirical results. Does this mean that the event is​ impossible?

What is the probability of an event that is​ impossible?  ____ ​(Type an integer or a​ decimal.)

Suppose that a probability is approximated to be zero based on empirical results. Does this mean that the event is​ impossible?

1. Yes
2. No

 

2.  What does it mean for an event to be​ unusual? Why should the cutoff for identifying unusual events not always be​ 0.05?

Choose the correct answer below.

1. An event is unusual if it has a probability equal to 0. The choice of a cutoff should consider the context of the problem.
2. An event is unusual if it has a high probability of occurring. The choice of the cutoff should consider the context of the problem.
3. An event is unusual if it has a probability equal to 1. The choice of a cutoff should consider the context of the problem.
4. An event is unusual if it has a low probability of occurring. The choice of a cutoff should consider the context of the problem.

 

3  True or  False​:

In a probability​ model, the sum of the probabilities of all outcomes must equal 1.

Choose the correct answer below.

1. False
2. True

 

4.   Determine if the following statement is true or false.

Probability is a measure of the likelihood of a random phenomenon or chance behavior.

Choose the correct answer below.

1. False
2. True

 

5.   Fill in the blank.

In​ probability, a(n)​ ________ is any process that can be repeated in which the results are uncertain.

 

6.   Fill in the blank below.  ​A(n) ______ is any collection of outcomes from a probability experiment.

 

7.  Is the following a probability​ model? What do we call the outcome ​”green​”?

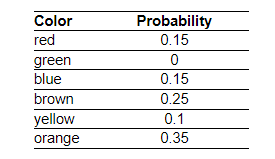
Is the table above an example of a probability​ model?

1. ​No, because not all the probabilities are greater than 0.
2. Yes, because the probabilities sum to 1.
3. No, because the probabilities do not sum to 1.
4. Yes​, because the probabilities sum to 1  and they are all greater than or equal  to 0 and less than or equal to 1.

 

What do we call the outcome ​”green​”?

1. Certain event
2. Not so unusual event
3. Unusual event
4. Impossible event

 

8.   Why is the following not a probability​ model?

Determine why it is not a probability model. Choose the correct answer below.

1. This is not a probability model because at least one probability is greater than 1.
2. This is not a probability model because the sum of the probabilities is not 1.
3. This is not a probability model because at least one probability is less than 0.
4. This is not a probability model because at least one probability is greater than 0.

 

9.  In a certain card​ game, the probability that a player is dealt a particular hand is 0.31.

Explain what this probability means. If you play this card game 100​ times, will you be dealt this hand exactly 31 ​times? Why or why​ not? Choose the correct answer below.

1. The probability 0.31 means that approximately 31 out of every 100 dealt hands will be that particular hand.​ No, you will not be dealt this hand exactly 31 times since the probability refers to what is expected in the​ short-term, not​ long-term.
2. The probability 0.31 means that exactly 31 out of every 100 dealt hands will be that particular hand.​ Yes, you will be dealt this hand exactly 31 times since the probability refers to​ short-term behavior, not​ long-term.
3. The probability 0.31 means that approximately 31 out of every 100 dealt hands will be that particular hand.​ No, you will not be dealt this hand exactly 31 times since the probability refers to what is expected in the​ long-term, not​ short-term.
4. The probability 0.31 means that exactly 31 out of every 100 dealt hands will be that particular hand.​ Yes, you will be dealt this hand exactly 31 times since the probability refers to​ long-term behavior, not​ short-term.

 

10.  Suppose you toss a coin 100 times and get 57 heads and 43 tails. Based on these​ results, what is the probability that the next flip results in a tail​?

The probability that the next flip results in a tail is approximately _______  (Type an integer or decimal rounded to two decimal places as​ needed.)

 

11.  Bob is asked to construct a probability model for rolling a pair of fair dice. He lists the outcomes as​ 2, 3,​ 4, 5,​ 6, 7,​ 8, 9,​ 10, 11, 12. Because there are 11​ outcomes, he​ reasoned, the probability of rolling a four must be

$\frac{1}{11}$

.  What is wrong with​ Bob’s reasoning?

Choose the correct answer below.

1. The sum of the probabilities of all outcomes does not equal 1.
2. The probability of an event is less than 0.
3. The experiment does not have equally likely outcomes.
4. The probability of an event is greater than 1.

 

12.  If a person rolls a six-sided die and then flips a coin​, describe the sample space of possible outcomes using 1, 2, 3, 4, 5, 6 for the die outcomes and H, T for the coin outcomes.​ (Make sure your answers reflect the order​ stated.)

The sample space is S=

 

13.   Let the sample space be S={1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.

Suppose the outcomes are equally likely. Compute the probability of the event E=​”an odd number less than 7​.”

P(E) =

 

14.   A survey of 200 randomly selected high school students determined that 23 play organized sports.

​(a) What is the probability that a randomly selected high school student plays organized​ sports?

​(b) Interpret this probability.

​(a) The probability that a randomly selected high school student plays organized sports is ___ ​(Round to the nearest thousandth as​ needed.)

​(b) Choose the correct answer below.

If​ 1,000 high school students were​ sampled, it would be expected that exactly _____ of them play organized sports.

If​ 1,000 high school students were​ sampled, it would be expected that about ____ of them play organized sports.

 

15. A bag of 100 tulip bulbs purchased from a nursery contains 40 red tulip​ bulbs, 40 yellow tulip​ bulbs, and 20 purple tulip bulbs

 ​(a) The probability that a randomly selected tulip is red is _____

 (b) The probability that a randomly selected tulip bulb is purple is _____  (Type an integer or a decimal. Do not​ round.)

​(c) Select the correct choice below and fill in the answer boxes within your choice. ​(Type whole​ numbers.)

If 100 tulip bulbs were sampled with​ replacement, one would expect about _____ of the bulbs to be red and about _____ of the bulbs to be purple.

If 100 tulip bulbs were sampled with​ replacement, one would expect exactly ____ of the bulbs to be red and exactly  _____ of the bulbs to be purple.

 

16.  In a national survey college students were​ asked, “How often do you wear a seat belt when riding in a car driven by someone​ else?” The response frequencies appear in the table to the right.​ (a) Construct a probability model for​ seat-belt use by a passenger.​ (b) Would you consider it unusual to find a college student who never wears a seat belt when riding in a car driven by someone​ else?

(a) Complete the table below.

Response	Probability
Never
Rarely
Sometimes
Most of the time
Always

​(b) Would you consider it unusual to find a college student who never wears a seat belt when riding in a car driven by someone​ else?

1. ​No, because the probability of an unusual event is 0.
2. ​Yes, because 0.01<​P(never)<0.10.
3. ​Yes, because ​P(never)<0.05.
4. ​No, because there were 104 people in the survey who said they never wear their seat belt.

 

17.  Clarice, Dominique, Roberto, John, and Marco work for a publishing company.  The company wants to send two employees to a statistics conference. To be​ fair, the company decides that the two individuals who get to attend will have their names randomly drawn from a hat.

​(a) Choose the correct answer below. Note that each person is represented by the first letter in their name.

1. CD, CR, CJ, CM
2. CD,CR,CJ,CM,DR,DJ,DM,RJ,RM,JM,DC,RC,JC,MC,RD,JD,MD,JR,MR,MJ
3. CD, CR, CJ, CM, DR, DJ, DM, RJ, RM, JM

​(b) The probability that Roberto and John attend the conference is ____  (Round to one decimal place as​ needed.)

​(c) The probability that Dominique attends the conference is ______  (Round to one decimal place as​ needed.)

​(d) The probability that Marco stays home is _______  (Round to one decimal place as​ needed.)

 

18 .  A baseball player hit 51 home runs in a season. Of the 51 home​ runs, 16 went to right​ field,

18 went to right center​ field, 8 went to center​ field, 8 went to left center​ field, and 1 went to left field.

​(a) The probability that a randomly selected home run was hit to right field is ______  (Round to three decimal places as​ needed.)

​(b) The probability that a randomly selected home run was hit to left field is ______  (Round to three decimal places as​ needed.)

​(c) Was it unusual for this player to hit a home run to left​ field?

1. ​No, because this player hit 1 home runs to left field.
2. ​Yes, because​ P(left ​field)<0.5.
3. ​No, because the probability of an unusual event is 0.
4. ​Yes, because​ P(left ​field)<0.05.

 

19.   The table shows the results of rolling a fair​ six-sided die. Complete parts ​(a) through ​(d) below.

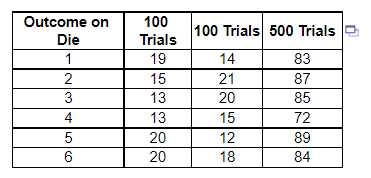
​(a) Using the​ table, find the empirical probability of rolling a 6 for the first 100 trials.

The empirical probability of rolling a 6 for the first 100 trials is ______  (Round to two decimal places as​ needed.)

​(b) Using the​ table, find the empirical probability of rolling a 6 for the second 100 trials.The empirical probability of rolling a 6 for second 100 trials is ______

(c) Using the​ table, find the empirical probability of rolling a 6 for 500 trials.

The empirical probability of rolling a 6 for 500 trials is _____  (Round to two decimal places as​ needed.)

​(d) Compare the empirical probabilities to the probability obtained using the classical​ method, and explain what they show. Choose the correct answer below.

1. All the empirical probabilities are equal to the classical probability. This is an outcome expected according to the Law of Large Numbers.
2. The empirical probabilities approach the classical probability as the sample size increases. This is an outcome expected according to the Law of Large Numbers.
3. The empirical probabilities are all equally far away from the classical probability. This is an outcome expected according to the Law of Large Numbers.
4. The empirical probability is closest to the classical probability for the two sets of 100 trials and gets farther away for the 500 trials. This is an outcome expected according to the Law of Large Numbers.

 

20.  Determine whether the probabilities below are computed using the classical​ method, empirical​ method, or subjective method. Complete parts ​(a) through ​(d) below.

​(a) The probability of having six girls in an six​-child family is 0.015625.

1. Classical method
2. Empirical method
3. Subjective method
4. It is impossible to determine which method is used.

​(b) On the basis of a survey of 1000 families with six ​children, the probability of a family having six girls is 0.0055.

1. Empirical method
2. Classical method
3. Subjective method
4. It is impossible to determine which method is used.

​(c) According to a sports​ analyst, the probability that a football team will win the next game is 0.35.

1. Classical method
2. Subjective method
3. Empirical method
4. It is impossible to determine which method is used.

​(d) On the basis of clinical​ trials, the probability of efficacy of a new drug is 0.73.

1. Classical method
2. Empirical method
3. Subjective method
4. It is impossible to determine which method is used.

 

21  You suspect a​ 6-sided die to be loaded and conduct a probability experiment by rolling the die 400 times. The outcome of the experiment is listed in the following table. Do you think the die is​ loaded? Why?

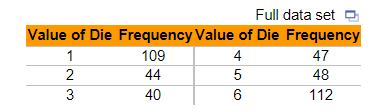
Do you think the die is​ loaded?

1. Yes, because two of the values have a higher probability of occurring than expected under the assumption of equally likely outcomes.
2. No, because each value has an approximately equal chance of occurring.
3. ​Yes, because the probabilities are not the same.

 

22.   In a recent​ survey, it was found that the median income of families in country A was ​$57,400. What is the probability that a randomly selected family has an income

less than ​$57,400​? What is the probability that a randomly selected family has an incomeless than $57,400​?

 

23. Explain the Law of Large Numbers. How does this law apply to gambling​ casinos? Choose the correct answer below.

1. As the number of repetitions of a probability experiment​ increases, the proportion with which a certain outcome is observed gets closer to 0. Casinos use the Law of Large Numbers to determine how many players gamble in certain games.
2. As the number of repetitions of a probability experiment​ increases, the proportion with which a certain outcome is observed gets closer to the probability of the outcome. This applies to casinos because they are able to make a profit in the long run because they have a small statistical advantage in each game.
3. As the number of repetitions of a probability experiment​ increases, the proportion with which a certain outcome is observed gets closer to the probability of the outcome. Casinos use the Law of Large Numbers to determine how many players gamble in certain games.
4. As the number of repetitions of a probability experiment​ increases, the proportion with which a certain outcome is observed gets closer to 1. This applies to casinos because they are able to make a profit in the long run because they have a small statistical advantage in each game.