Homework 4.1

1. The road mileage between City M and several selected cities is shown in the table. If we consider this as a function that pairs each city with a​ distance, is the function a​ one-to-one function?

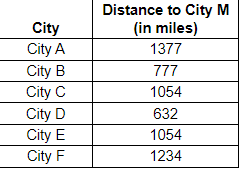
Is the function a​ one-to-one function?

1. No
2. Yes

2.   Fill in the blank.

For a function to have an​ inverse, it must be​ ________.

3.   Select the correct choices that complete the sentence below.  If two functions f and g are​ inverses, then 

= ______ and ____________ = x

4.   Fill in the blank to correctly complete the sentence below.

If ​f(x)=x3​, then

5.   Determine whether the function graphed is​ one-to-one.

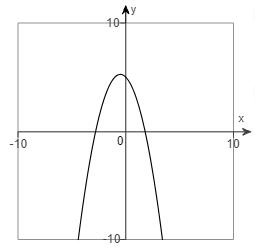
Is the function graphed​ one-to-one?

1. ​Yes, because each​ x-value corresponds to only one​ y-value, and each​ y-value corresponds to only one​ x-value.
2. ​No, there is a horizontal line that intersects the graph at more than one point.
3. ​No, because each​ x-value corresponds to every​ y-value, and each​ y-value corresponds to every​ x-value.
4. ​Yes, every horizontal line intersects the graph at exactly one point.

6.  Determine whether the function is​ one-to-one.

Is the function​ one-to-one? Select the correct choice below​ and, if​ necessary, fill in the answer boxes to complete your choice.

1. ​No, because the​ f(x) value 2 corresponds to two​ x-values _____ and _____
2. ​Yes, because each​ x-value corresponds to only one​ f(x) value, and each​ f(x) value corresponds to only one​ x-value.

7.  Use the definition of inverses to determine whether f and g are inverses.                                               

f(x)=3x−9​,

g(x)=

+3

Are the f and g inverses of each​ other?

1. Yes
2. No

8.  Use the definition of inverses to determine whether f and g are inverses.

f(x)=−3x+11​,

g(x)=

x−11

Are the given functions​ inverses?

1. No
2. Yes