Exam 2

1. The cost (in dollars) of producing x units of a certain commodity is C(x) = 2,000 + 5x + 0.05x².

(a) Find the average rate of change (in $ per unit) of C with respect to x when the production level is changed from x = 100 to the given value. (Round your answers to the nearest cent.)

(b) Find the instantaneous rate of change (in $ per unit) of C with respect to x when x = 100.   (This is called the marginal cost. Its significance will be explained in a future chapter.)

2.   Find equations of the two tangent lines to the graph of f(x) = x² that pass through the point (-1, -3).

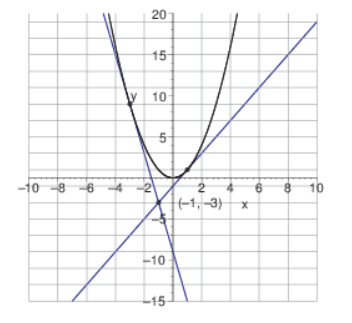
Line with negative slope, y=

Line with positive slope, y=

3.   The limit represents the derivative of some function f at some number a. State such an f and a.

$\underset{h\to 0}{\lim }\frac{{\left(1+h\right)}^8–1}{h}$

4.   Determine the point(s) (if any) at which the graph of the function has a horizontal tangent line.

5.  The graph of f is given. State the numbers at which f is not differentiable. (Enter your answers as a comma-separated list.)

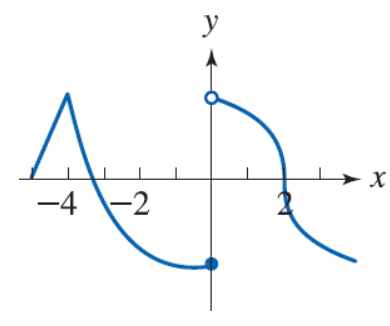
x =

6.   Find constants A and B such that the function y = A sin(x) + B cos(x)  satisfies the differential equation  y” + y’ − 9y = sin(x).

A =

B =

7.   Find the points on the curve y = x³ + 3x² − 9x + 2  where the tangent is horizontal.

smaller x value (x,y) =

Larger x value  (x,y) =

8. Differentiate.

$f\left(t\right) =\frac{\sqrt[3]{t}}{t–3}$

$f‘\left(t\right)=$

9.  Let the function f be defined by

$f\left(x\right)=\frac{\tan \left(x\right)–1}{sec\left(x\right)}$

(a) Use the Quotient Rule to differentiate the function f ‘(x).

(b) Simplify the expression for f(x) by writing it in terms of sin(x) and cos(x), and then find f ‘(x).

(c) Show that your answers to parts (a) and (b) are equivalent?

1. Yes
2. No

10.  Sketch the graph of f ‘.

Explain how you found your answer.

The slope of the graph of f is  ______  for x < 0  and _____ for x > 0.    The slope is _____ at 0

11.  Find f ‘(a).

$f\left(t\right)=\frac{2t+16}{t+9}$

f ‘(a)

12 Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false.

If a function is continuous at a point, then it is differentiable at that point.

13   Find an equation of the tangent line to the graph of  y = g(x) at x = 2 if g(2) = −5 and g’(2) = 4.   (Enter your answer as an equation in terms of y and x.)

14  A graphing calculator is recommended.

Let y = 12x sin(x).

(a) Find an equation of the tangent line to the curve y at the point

y=

(b) Illustrate part (a) by graphing the curve y and the tangent line on the same screen.

15.  A curve has equation y = f(x).

(a)  Write an expression for the slope of the secant line through the points 

P(2, f(2))  and Q(x, f(x)).

(b) Write an expression for the slope of the tangent line at P.

16. The limit represents f ‘(c) for a function f(x) and a number c. Find f(x) and c.

f(x)=

c=

17.   A ball is thrown into the air with a velocity of 37 ft/s. Its height, in feet, after t seconds is given by s(t) = 37t − 16t².

 Find the velocity (in ft/s) of the ball at time t = 1 second.

18.   Find the derivative of the function using the definition of derivative.

$g\left(x\right)=\sqrt{5–x}$

g'(x) =

19.  Differentiate the function after first rewriting the function in a different form. (Do not use the product or quotient rules.)

$P\left(w\right)=\frac{8w^2–6w+4}{\sqrt{w}}$

P'(w) =

20 .