Navigation » List of Schools, Subjects, and Courses » Math 227 – Statistics » Quizzes » Chapter 5 Quiz
No Answers We dont have answer to this question yet. If you need help with your homework send us an email  or chat with our tutors
or chat with our tutors
Chapter 5 Quiz
Chapter 5 Quiz
1. In a recent poll, a random sample of adults in some country (18 years and older) was asked, “When you see an ad emphasizing that a product is “Made in our country,” are you more likely to buy it, less likely to buy it, or neither more nor less likely to buy it?” The results of the survey, by age group, are presented in the following contingency table. Complete parts (a) through (c).
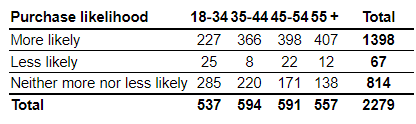
(a) What is the probability that a randomly selected individual is 45 to 54 years of age, given the individual is less likely to buy a product emphasized as “Made in our country”?
The probability is approximately _______ (Round to three decimal places as needed.)
(b) What is the probability that a randomly selected individual is less likely to buy a product emphasized as “Made in our country,” given the individual is 45 to 54 years of age?
The probability is approximately ______ (Round to three decimal places as needed.)
(c) Are 18- to 34-year-olds more likely to buy a product emphasized as “Made in our country” than individuals in general?
- Yes, more likely
- No, less likely
2. The probability that a randomly selected 2-year-old male feral cat will live to be 3 years old is 0.96685.
(a) What is the probability that two randomly selected 2-year-old male feral cats will live to be 3 years old?
(b) What is the probability that six randomly selected 2-year-old male feral cats will live to be 3 years old?
(c) What is the probability that at least one of six randomly selected 2-year-old male feral cats will not live to be 3 years old? Would it be unusual if at least one of six randomly selected 2-year-old male feral cats did not live to be 3 years old?
(a) The probability that two randomly selected 2-year-old male feral cats will live to be 3 years old is ____________ (Round to five decimal places as needed.)
(b) The probability that six randomly selected 2-year-old male feral cats will live to be 3 years old is ___________ (Round to five decimal places as needed.)
(c) The probability that at least one of six randomly selected 2-year-old male feral cats will not live to be 3 years old is _____________ (Round to five decimal places as needed.)
Would it be unusual if at least one of six randomly selected 2-year-old male feral cats did not live to be 3 years old? __________ because the probability of this happening is _________ 0.05.
3. The data in the following table show the association between cigar smoking and death from cancer for 135,387 men. Note: current cigar smoker means cigar smoker at time of death.
(a) P(died from cancer) = _________ (Round to three decimal places as needed.)
(b) P(current cigar smoker) = ________ (Round to three decimal places as needed.)
(c) P(died from cancer and current cigar smoker) = ___________ (Round to three decimal places as needed.)
(d) P(died from cancer or current cigar smoker) = __________ (Round to three decimal places as needed.)
4. Find the probability
if P(E)=0.18.
The probability
) is __________
5. Let the sample space be S={1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
Suppose the outcomes are equally likely. Compute the probability of the event E=”an even number less than 8.”
6. Let the sample space be S={1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Suppose the outcomes are equally likely. Compute the probability of the event E=”an even number less than 8.”
A probability experiment is conducted in which the sample space of the experiment is S={5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16}, event F={7, 8, 9, 10, 11, 12}, and event G={11, 12, 13, 14}.
Assume that each outcome is equally likely. List the outcomes in F or G. Find P(F or G) by counting the number of outcomes in F or G. Determine P(F or G) using the general addition rule.
List the outcomes in F or G. Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
7. Fill in the blank.
Two events E and F are ________ if the occurrence of event E in a probability experiment does not affect the probability of event F.
8. True or False:
In a probability model, the sum of the probabilities of all outcomes must equal 1.
Choose the correct answer below.
- True
- False
9. A test to determine whether a certain antibody is present is 99.3% effective. This means that the test will accurately come back negative if the antibody is not present (in the test subject) 99.3% of the time. The probability of a test coming back positive when the antibody is not present (a false positive) is 0.007. Suppose the test is given to six randomly selected people who do not have the antibody.
(a) What is the probability that the test comes back negative for all six people?
(b) What is the probability that the test comes back positive for at least one of the six people?
(a) P(all 6 tests are negative) = _______ (Round to four decimal places as needed.)
(b) P(at least one positive) = ________ (Round to four decimal places as needed.)
10. Suppose that two cards are randomly selected from a standard 52-card deck.
(a) What is the probability that the first card is a king and the second card is a king if the sampling is done without replacement?
(b) What is the probability that the first card is a king and the second card is a king if the sampling is done with replacement?
(a) If the sampling is done without replacement, the probability that the first card is a king and the second card is a king is ____________ (Round to three decimal places as needed.)
(b) If the sampling is done with replacement, the probability that the first card is a king and the second card is a king is __________ (Round to three decimal places as needed.)
 or chat with our tutors
or chat with our tutors
