Exam 2

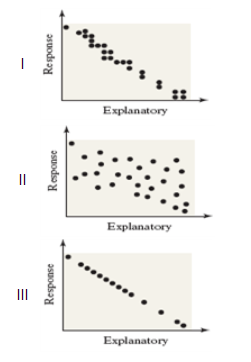
1. Match the linear correlation coefficient to the scatter diagram. The scales on the​ x- and​ y-axis are the same for each scatter diagram. 

(a) r = -0.049 , (b) r = -0.922 , (c) r = -1
​

2.   Classify the following random variable as either discrete or continuous. The number of emails received on any given day

1. Continuous
2. Discrete

3.  The data below are the ages and systolic blood pressures​ (measured in millimeters of​ mercury) of 9 randomly selected adults. What is the best predicted value for y given x=62?

Round to the nearest whole number.

1. 155
2. 151
3. 148
4. 153

4  Consider a political discussion group consisting of 3 ​Democrats, 5 ​Republicans, and 6 Independents. Suppose that two group members are randomly​ selected, in​ succession, to attend a political convention. Find the probability of selecting an Independent and then a Democrat. Express your answer as a simplified fraction.

5.  If p is the probability of success of a binomial​ experiment, what is the probability of​ failure?

6. Use the discrete probability distribution below to find the probability that x equals 4.

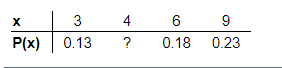
1. 0.54
2. 1.84
3. 0.1341
4. 0.46

7. A probability experiment is conducted in which the sample space of the experiment is S={3,4,5,6,7,8,9,10,11,12,13}. Let event A={6,7,8,9,10}.

Assume that each outcome is equally likely. List the outcomes in Ac. Find ​P(Ac​).

8.  A machine has four​ components, A,​ B, C, and​ D, set up in such a manner that all four parts must work for the machine to work properly. Assume the probability of one part working does not depend on the functionality of any of the other parts. Also assume that the probabilities of the individual parts working are ​P(A)=​P(B)=0.97​, ​P(C)=0.99​, and ​P(D)=0.93. Find the probability that at least one of the four parts will work. Round to six decimal places.

1. 0.99999
2. 0.133713
3. 0.000001
4. 0.866287

9.

The table below describes the exercise habits of a group of people suffering from high blood pressure. If a woman is selected at random from the​ group, find the probability that she does not exercise. Round to three decimal places.

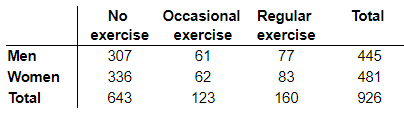
1. 0.523
2. 0.363
3. 0.519
4. 0.699

10 A poll reported that 66​% of adults were satisfied with the job the major airlines were doing. Suppose 15 adults are selected at random and the number who are satisfied is recorded. Complete parts​ (a) through​ (e) below.

1. This is a binomial experiment because there are two mutually exclusive outcomes for each​ trial, there is a random number of​ trials, the outcome of one trial does not affect the outcome of​ another, and the probability of success is the same for each trial.
2. This is a binomial experiment because there are three mutually exclusive outcomes for each​ trial, there is a fixed number of​ trials, the outcome of one trial does not affect the outcome of​ another, and the probability of success is the same for each trial
3. This is a binomial experiment because there are two mutually exclusive outcomes for each​ trial, there is a fixed number of​ trials, the outcome of one trial does not affect the outcome of​ another, and the probability of success is the same for each trial.
4. This is a binomial experiment because there are two mutually exclusive outcomes for each​ trial, there is a fixed number of​ trials, the outcome of one trial does not affect the outcome of​ another, and the probability of success changes in each trial.

Interpret the probability. Select the correct choice below and fill in the answer box within your choice.
​(Round to the nearest integer as​ needed.) 

1. In 100 randomly sampled surveys of  ​adults,  or more of the  adults would be expected to be satisfied with the airlines in about 
   enter your response here of those surveys.
2. In 100 randomly sampled surveys of  ​adults, exactly  out of the  adults would be expected to be satisfied with the airlines in about 
   ___  of those surveys.
3. In 100 randomly sampled surveys of  ​adults, less than  of the  adults would be expected to be satisfied with the airlines in about enter your response here of those surveys.

(c) Find and interpret the probability that at least  of them are satisfied with the airlines.
The probability that at least  adults are satisfied with the airlines is ____. 
​(Round to four decimal places as​ needed.)

Interpret the probability. Select the correct choice below and fill in the answer box within your choice.
​(Round to the nearest integer as​ needed.) 

1. In 100 randomly sampled surveys of  ​adults,  or more of the  adults would be expected to be satisfied with the airlines in about 19 of those surveys.
2. In 100 randomly sampled surveys of  ​adults, exactly  out of the  adults would be expected to be satisfied with the airlines in about enter your response here of those surveys.
3. In 100 randomly sampled surveys of  ​adults, less than  of the  adults would be expected to be satisfied with the airlines in about enter your response here of those surveys.

​(d) Find and interpret the probability that between  and  of​ them, inclusive, are satisfied with the airlines.
The probability that between  and  ​adults, inclusive, are satisfied with the airlines is ____ (Round to four decimal places as​ needed.)

Interpret the probability. Select the correct choice below and fill in the answer box within your choice.
​(Round to the nearest integer as​ needed.) 

1. In 100 randomly sampled surveys of  ​adults, no more than  or no less than  out of the  adults would be expected to be satisfied with the airlines in about 
   enter your response here of those surveys.
2. In 100 randomly sampled surveys of  ​adults, between  and  of the  adults would be expected to be satisfied with the airlines in about 
   39 of those surveys.
3. In 100 randomly sampled surveys of  ​adults, either  or  of the  adults would be expected to be satisfied with the airlines in about 
   enter your response here of those surveys.

(e) Would it be unusual to find more than  who are satisfied with the job the major airlines were​ doing?
The result _____  ​unusual, because

under the assumption that the proportion of adults that are satisfied with the airlines is 66​%. ​Thus, in 100 random samples of size ​, this result is expected in about 7 of the random samples.
​(Type integers or decimals. Round to four decimal places as​ needed.)

11.  A scatter diagram locates a point in a two dimensional plane. The diagram locates the​ _______ variable on the horizontal axis and the​ _______ variable on the vertical axis. 

1. ​response; explanatory
2. ​study; explanatory
3. ​explanatory; response
4. ​response; study

12. Twelve  jurors are randomly selected from a population of  million residents. Of these  million​ residents, it is known that ​% are of a minority race. Of the  jurors​ selected,  are minorities.
​(a) What proportion of the jury described is from a minority​ race?
​(b) If  jurors are randomly selected from a population where ​% are​ minorities, what is the probability that  or fewer jurors will be​ minorities?
​(c) What might the lawyer of a defendant from this minority race​ argue?
​(a) The proportion of the jury described that is from a minority race is _____ (Round to two decimal places as​ needed.)
​(b) The probability that  or fewer out of  jurors are​ minorities, assuming that the proportion of the population that are minorities is ​%, is ____ ​(Round to four decimal places as​ needed.) 
​(c) Choose the correct answer below.

1. The number of minorities on the jury is unusually​ low, given the composition of the population from which it came.
2. The number of minorities on the jury is​ impossible, given the composition of the population from which it came.
3. The number of minorities on the jury is unusually​ high, given the composition of the population from which it came.
4. The number of minorities on the jury is​ reasonable, given the composition of the population from which it came.

13.   ​A(n) _______________ of a probability experiment is the collection of all outcomes possible.

1. Sample space
2. Bernoulli space
3. Prediction set
4. Event set

14.   The data below are the final exam scores of 10 randomly selected history students and the number of hours they slept the night before the exam. Find the equation of the regression line for the given data. What would be the predicted score for a history student who slept 15 hours the previous​ night? Is this a reasonable​ question? Round your predicted score to the nearest whole number. Round the regression line values to the nearest hundredth.

15. A card is dealt fro m a​ 52-card deck. Find the probability that it is not a 6. Express the probability as a simplified fraction.

16. An instructor wishes to determine if there is a relationship between the number of absences from his class and a​ student’s final grade in the course. What is the explanatory​ variable?

1. The​ instructor’s point scale for attendance
2. ​Student’s performance on the final examination
3. Final Grade
4. Absences

17. If two events have no outcomes in common they are said to be​ ____________.

1. Independent
2. Conditional
3. Disjoint
4. At odds

18.