Test 2

1. Find an equation for the tangent line to the graph of

The equation of the tangent line is y=

2.

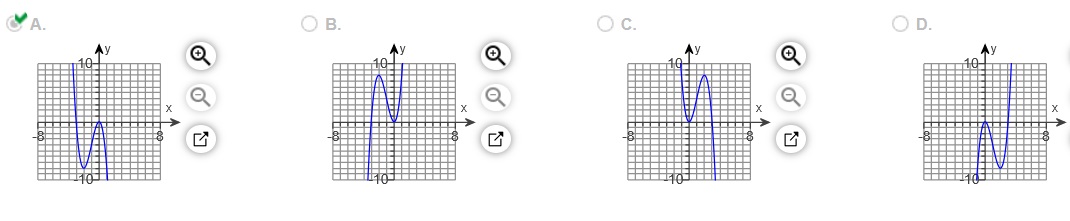
3. Find the relative extreme points of the​ function, if they exist. Then sketch a graph of the function. 

1. The relative minimum​ point(s) is/are______
2. There are no relative minimum points

1. The relative maximum​ point(s) is/are _______
2. There are no relative maximum points.

Choose the correct graph below.

4.  Sketch the graph of the following function. List the coordinates of where extrema or points of inflection occur. State where the function is increasing or decreasing as well as where it is concave up or concave down.

$f\left(x\right) = x^3–3x^2–72x$

What are the coordinates of the relative​ extrema? Select the correct choice below​ and, if​ necessary, fill in the answer box to complete your choice.

1. The coordinates of the relative extrema are ____
2. There are no relative extrema.

What are the coordinates of the inflection​ points? Select the correct choice below​ and, if​ necessary, fill in the answer box to complete your choice.

1. The coordinates of the inflection points are ____
2. There are no inflection points.

Choose the correct graph below.

5. Find the absolute maximum and minimum values of each function over the indicated​ interval, and indicate the​ x-values at which they occur.

$f\left(x\right) = 2x^3–x^2–4x+12; \left[–1,0\right]$

The absolute maximum value is

The absolute minimum value is

6.   Find the maximum profit and the number of units that must be produced and sold in order to yield the maximum profit. Assume that​ revenue, R(x), and​ cost, C(x), of producing x units are in dollars.

7.  Let​ R(x), C(x), and​ P(x) be,​ respectively, the​ revenue, cost, and​ profit, in​ dollars, from the production and sale of x items. If R (x) = 4x and C(x) =

. 

find each of the following.

a. P(x)

b. R(200), C (200), and P(200)

(c) R'(x), C'(x), and P'(x)

(d) R'(200), C'(200), and P'(200)

8.  Use implicit differentiation to find dy / dx.  Then find the slope of the curve at the given point.

$5xy–3x+y=7; \left(–2, –\frac{1}{9}\right)$

9.  Differentiate the following function.

$f\left(x\right)=7+8e^{2x}$

$f‘\left(x\right) =$

10.  Differentiate

$f\left(x\right)= x^7–3e^{4x}$

$f‘\left(x\right) =$