Navigation » List of Schools, Subjects, and Courses » Math 227 – Statistics » Quizzes » Chapter 6 Quiz
No Answers We dont have answer to this question yet. If you need help with your homework send us an email  or chat with our tutors
or chat with our tutors
Chapter 6 Quiz
Chapter 6 Quiz
1. In the following probability distribution, the random variable x represents the number of activities a parent of a K to 5th-grade student is involved in. Complete parts (a) through (f) below.
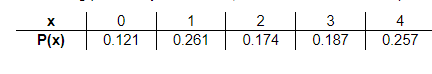
(a) Verify that this is a discrete probability distribution.
This is a discrete probability distribution because the sum of the probabilities is ____ and each probability is _______
(b) Graph the discrete probability distribution. Choose the correct graph below.

(c) Compute and interpret the mean of the random variable x.
The mean is ___ activities. (Type an integer or a decimal. Do not round.)
Which of the following interpretations of the mean is correct?
- The observed value of an experiment will be equal to the mean of the random variable in most experiments.
- As the number of experiments decreases, the mean of the observations will approach the mean of the random variable.
- The observed value of an experiment will be less than the mean of the random variable in most experiments.
- As the number of experiments increases, the mean of the observations will approach the mean of the random variable.
(d) Compute the standard deviation of the random variable x.
The standard deviation is _____ activities. (Round to one decimal place as needed.)
(e) What is the probability that a randomly selected student has a parent involved in three activities?
The probability is ____ (Type an integer or a decimal. Do not round.)
(f) What is the probability that a randomly selected student has a parent involved in three or four activities?
The probability is ____ 0.444. (Type an integer or a decimal. Do not round.)
2. No Answers We dont have answer to this question yet. If you need help with your homework send us an email or chat with our tutors
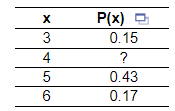
P(4) = _____
3. Determine whether the following probability experiment represents a binomial experiment and explain the reason for your answer. An experimental drug is administered to 120 randomly selected individuals, with the number of individuals responding favorably recorded. Does the probability experiment represent a binomial experiment?
- No, because there are more than two mutually exclusive outcomes for each trial.
- No, because the trials of the experiment are not independent.
- No, because the probability of success differs from trial to trial.
- Yes, because the experiment satisfies all the criteria for a binomial experiment.
4. What is the formula for the expected number of successes in a binomial experiment with n trials and probability of success p?
Choose the correct forumla below.
5. Determine whether the random variable is discrete or continuous. In each case, state the possible values of the random variable.
(a) The number of customers arriving at a bank between noon and 1:00 P.M.
(b) The .amount of snowfall
(a) Is the number of discrete or continuous?
- The random variable is discrete. The possible values are
- The random variable is continuous. The possible values are
.
- The random variable is discrete. The possible values are x=0, 1, 2,…
- The random variable is continuous. The possible values are x=0, 1, 2,…
(b) Is the discrete or continuous?
- The random variable is continuous. The possible values are s=1,2,3…
- The random variable is discrete. The possible values are s=1,2,3….
- The random variable is discrete. The possible values are
- The random variable is continuous. The possible values are
.
6. The following data represent the number of games played in each series of an annual tournament from 1929 to 2005 . Complete parts (a) through (d) below.
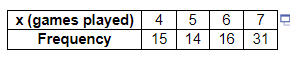
(a) Construct a discrete probability distribution for the random variable x.
| x (games played) | P(x) |
| 4 | |
| 5 | |
| 6 | |
| 7 |
(b) Graph the discrete probability distribution. Choose the correct graph below.

7. A binomial probability experiment is conducted with the given parameters. Compute the probability of x successes in the n independent trials of the experiment.
n = 11, p=0.2,
The probability of successes is
. (Round to four decimal places as needed.)
 or chat with our tutors
or chat with our tutors
