Navigation » List of Schools, Subjects, and Courses » Math 136 – Introduction to Statistics » Quiz » Quiz 4
No Answers We dont have answer to this question yet. If you need help with your homework send us an email  or chat with our tutors
or chat with our tutors
Quiz 4
Quiz 4
1. If a person draws a playing card and checks itssuit and then spins a three-space spinner, describe the sample space of possible outcomes using C, D, H, S for the card outcomes and 1, 2, 3, for the spinner outcomes.
The sample space is S = __________________–
2. The following table shows the distribution of murders by type of weapon for murder cases in a particular country over the past 12 years. Complete parts (a) through (e).
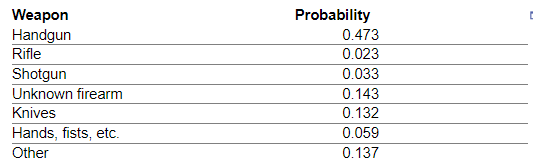
(a) Is the given table a probability model? Why or why not?
- No; the sum of the probabilities of all outcomes does not equal 1.
- No; the probability of all events in the table is not greater than or equal to 0 and less than or equal to 1, and the sum of the probabilities of all outcomes does not equal 1.
- No; the probability of all events in the table is not greater than or equal to 0 and less than or equal to 1.
- Yes; the rules required for a probability model are both met.
(b) What is the probability that a randomly selected murder resulted from a rifle or shotgun?
P(rifle or shotgun) = ______ (Type a decimal rounded to three decimal places as needed.)
Interpret this probability. Select the correct choice below and fill in the answer box to complete your choice.
- If 1000 murders were randomly selected, exactly ____ of them would have resulted from a rifle or shotgun.
- If 1000 murders were randomly selected, we would expect about ___ of them to have resulted from a rifle or shotgun.
(c) What is the probability that a randomly selected murder resulted from a handgun, rifle, or shotgun?
P(handgun, rifle, or shotgun) = ____ (Type a decimal rounded to three decimal places as needed.)
Interpret this probability. Select the correct choice below and fill in the answer box to complete your choice.
- If 1000 murders were randomly selected, exactly ____ of them would have resulted from a handgun, rifle, or shotgun.
- If 1000 murders were randomly selected, we would expect about ____ of them to have resulted from a handgun, rifle, or shotgun.
(e) Are murders with a shotgun unusual?
- No
- Yes
3. Explain the Law of Large Numbers. How does this law apply to gambling casinos? Choose the correct answer below.
- As the number of repetitions of a probability experiment increases, the proportion with which a certain outcome is observed gets closer to 1. This applies to casinos because they are able to make a profit in the long run because they have a small statistical advantage in each game.
- As the number of repetitions of a probability experiment increases, the proportion with which a certain outcome is observed gets closer to the probability of the outcome. This applies to casinos because they are able to make a profit in the long run because they have a small statistical advantage in each game.
- As the number of repetitions of a probability experiment increases, the proportion with which a certain outcome is observed gets closer to 0. Casinos use the Law of Large Numbers to determine how many players gamble in certain games.
- As the number of repetitions of a probability experiment increases, the proportion with which a certain outcome is observed gets closer to the probability of the outcome. Casinos use the Law of Large Numbers to determine how many players gamble in certain games.
4. In a national survey college students were asked, “How often do you wear a seat belt when riding in a car driven by someone else?” The response frequencies appear in the table to the right. (a) Construct a probability model for seat-belt use by a passenger. (b) Would you consider it unusual to find a college student who never wears a seat belt when riding in a car driven by someone else?

(a) Complete the table below.
| Complete the table below | |
| Response | Probability |
| Never | |
| Rarely | |
| Sometimes | |
| Most of the time | |
| Always |
(b) Would you consider it unusual to find a college student who never wears a seat belt when riding in a car driven by someone else?
- No, because the probability of an unusual event is 0.
- Yes, because 0.01 < P(never) < 0.10.
- No, because there were 145 people in the survey who said they never wear their seat belt.
- Yes, because P(never) < 0.05.
5. In a recent survey, it was found that the median income of families in country A was $57,800. What is the probability that a randomly selected family has an income greater than $57,800?
What is the probability that a randomly selected family has an income greater than $57,800? ____
6. Determine whether the probabilities below are computed using the classical method, empirical method, or subjective method. Complete parts (a) through (d) below.
(a) The probability of having girls in an -child family is 0.015625.
- Subjective method
- Empirical method
- Classical method
- It is impossible to determine which method is used.
(b) On the basis of a survey of 1000 families with six children, the probability of a family having six girls is 0.0059.
- Empirical method
- Subjective method
- Classical method
- It is impossible to determine which method is used.
(c) According to a sports analyst, the probability that a football team will win the next game is 0.39.
- Classical method
- Subjective method
- Empirical method
- It is impossible to determine which method is used.
(d) On the basis of clinical trials, the probability of efficacy of a new drug is 0.78.
- Subjective method
- Empirical method
- Classical method
- It is impossible to determine which method is used.
7. A standard deck of cards contains 52 cards. One card is selected from the deck.
(a) Compute the probability of randomly selecting a club or diamond.
(b) Compute the probability of randomly selecting a club or diamond or spade.
(c) Compute the probability of randomly selecting a thee or diamond.
(a) P( club or diamond) = _____ (Type an integer or a decimal rounded to three decimal places as needed.)
(b) P( club or diamond or spade) = ____ (Type an integer or a decimal rounded to three decimal places as needed.)
(c) P( three or diamond) = ____ (Type an integer or a decimal rounded to three decimal places as needed.)
8. Find the probability of the indicated event if P(E) = 0.40 and P(F) = 0.35.
Find P(E or F) if P(E and F) = 0.05.
P(E or F) = ____ (Simplify your answer.)
9. A survey of 200 randomly selected high school students determined that 17 play organized sports.
(a) What is the probability that a randomly selected high school student plays organized sports?
(b) Interpret this probability.
(a) The probability that a randomly selected high school student plays organized sports is ____ (Round to the nearest thousandth as needed.)
(b) Choose the correct answer below. (Type a whole number.)
- If 1,000 high school students were sampled, it would be expected that about ___ of them play organized sports.
- If 1,000 high school students were sampled, it would be expected that exactly ____ of them play organized sports.
 or chat with our tutors
or chat with our tutors
