Navigation » List of Schools, Subjects, and Courses » Math 110A – PreCalculus I » Homeworks » Section 2.8 Homework
No Answers We dont have answer to this question yet. If you need help with your homework send us an email  or chat with our tutors
or chat with our tutors
Section 2.8 Homework
Section 2.8 Homework
1. A function f is one-to-one if different inputs produce ______ outputs. You can tell from the graph that a function is one-to-one by using the _____ test
2. A function f has the following verbal description: “Multiply by 7, add 4, and then take the third power of the result.”
(b) Find algebraic formulas that express f and f −1 in terms of the input x.
3. A graph of a function f is given.

Does f have an inverse?
- No
- Yes
4. True or false?
(a) If f has an inverse, then f −1(x) is always the same as
(b) If f has an inverse, then f −1(f(x)) = x.
5. A graph of a function f is given.

Determine whether f is one-to-one.
6. A graph of a function f is given.
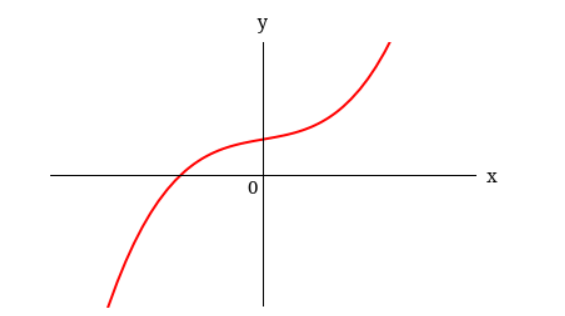
Determine whether f is one-to-one.
7. A graph of a function f is given.
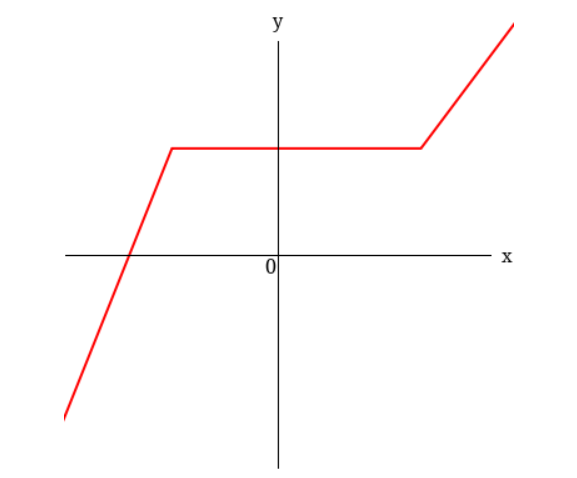
Determine whether f is one-to-one.
8. Determine whether the function is one-to-one.
9. Determine whether the function is one-to-one.
10. Determine whether the function is one-to-one. f(x) = x4 + 9
11. Assume that f is a one-to-one function.
(a) If f(4) = 9, find f −1(9).
(b) If f −1(8) = −1, find f(−1).
12. If g(x) = x2 + 4x with x ≥ −2, find g−1(21).
13. Use the Inverse Function Property to determine whether f and g are inverses of each other.
14. Use the Inverse Function Property to determine whether f and g are inverses of each other.
15. Find the inverse function of f. f(x) = 2 − 3x
16. Find the inverse function of f.
17. Find the inverse function of f.
A one-to-one function is given.
A one-to-one function is given.g(x) =
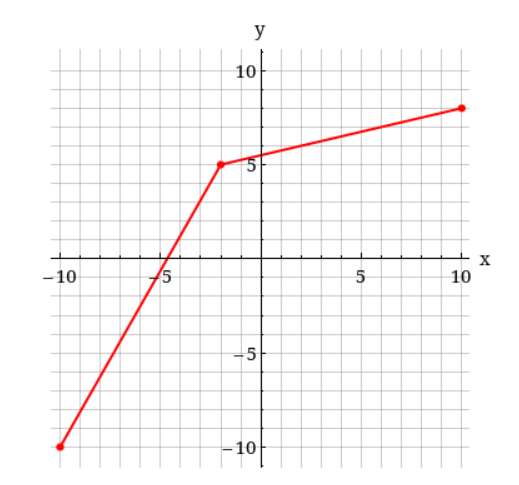
 or chat with our tutors
or chat with our tutors
