Exam 3

 

1.  In a test of the effectiveness of garlic for lowering​ cholesterol, 81 subjects were treated with raw garlic. Cholesterol levels were measured before and after the treatment. The changes​ (before minus​ after) in their levels of LDL cholesterol​ (in mg/dL) have a mean of 0.3 and a standard deviation of 1.82.  Use a 0.01 significance level to test the claim that with garlic​ treatment, the mean change in LDL cholesterol is greater than 0.  What do the results suggest about the effectiveness of the garlic​ treatment? Assume that a simple random sample has been selected. Identify the null and alternative​ hypotheses, test​ statistic, P-value, and state the final conclusion that addresses the original claim. 

 

What are the null and alternative​ hypotheses?

 

 

Determine the test statistic.   ____ ​(Round to two decimal places as​ needed.)

Determine the​ P-value.  ____  ​(Round to three decimal places as​ needed.)

State the final conclusion that addresses the original claim.  _____

$H_0$

.  There is ________ evidence to conclude that the mean of the population of changes ________ 0.

 

 

2. A simple random sample of​ front-seat occupants involved in car crashes is obtained. Among 2918 occupants not wearing seat​ belts, 38 were killed. Among 7681 
occupants wearing seat​ belts, 13 were killed. Use a 0.01 significance level to test the claim that seat belts are effective in reducing fatalities. Complete parts​ (a) through​ (c) below.
a. Test the claim using a hypothesis test.
Consider the first sample to be the sample of occupants not wearing seat belts and the second sample to be the sample of occupants wearing seat belts. What are the null and alternative hypotheses for the hypothesis​ test?

 

Identify the test statistic.  z= ______ ​(Round to two decimal places as​ needed.)

Identify the​ P-value.  ​P- value = ______ ​(Round to three decimal places as​ needed.)

What is the conclusion based on the hypothesis​ test?   The​ P-value is ______ the significance level of

$\alpha =0.01,$

so _____ the null hypothesis. There ___ sufficient evidence to support the claim that the fatality rate is higher for those not wearing seat belts.

b. Test the claim by constructing an appropriate confidence interval.   The appropriate confidence interval is ______ <

$(p_1 – p_2) <$

____ ​(Round to three decimal places as​ needed.) 

What is the conclusion based on the confidence​ interval?

Because the confidence interval limits _______ 0, it appears that the two fatality rates are ______.   Because the confidence interval limits include _____ ​values, it appears that the fatality rate is _______ for those not wearing seat belts.

c. What do the results suggest about the effectiveness of seat​ belts?

1. The results suggest that the use of seat belts is associated with lower fatality rates than not using seat belts.
2. The results suggest that the use of seat belts is associated with higher fatality rates than not using seat belts.
3. The results suggest that the use of seat belts is associated with the same fatality rates as not using seat belts. 
4. The results are inconclusive.

 

 

3.   A data set lists earthquake depths. The summary statistics are n = 500​, 

$\overline{x}$

= 5.78km, s = 4.45km. Use a 0.01 significance level to test the claim of a seismologist that these earthquakes are from a population with a mean equal to 5.00.  Assume that a simple random sample has been selected. Identify the null and alternative​ hypotheses, test​ statistic, P-value, and state the final conclusion that addresses the original claim.

What are the null and alternative​ hypotheses?

 

Determine the test statistic.  _____ ​(Round to two decimal places as​ needed.)

Determine the​ P-value. ​_____  (Round to three decimal places as​ needed.)

State the final conclusion that addresses the original claim.  _____

$H_0.$

There is _____ evidence to conclude that the mean of the population of earthquake depths is 5.00km  _____ correct.

 

4.   Data on the weights​ (lb) of the contents of cans of diet soda versus the contents of cans of the regular version of the soda is summarized to the right. Assume that the two samples are independent simple random samples selected from normally distributed​ populations, and do not assume that the population standard deviations are equal. Complete parts​ (a) and​ (b) below. Use a 0.01 significance level for both parts.

 

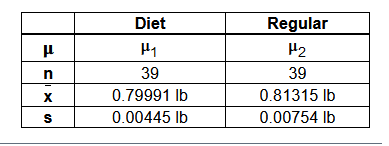
a. Test the claim that the contents of cans of diet soda have weights with a mean that is less than the mean for the regular soda.  What are the null and alternative​ hypotheses?

 

The test​ statistic, t, is ________ ​(Round to two decimal places as​ needed.)

The​ P-value is __________. ​(Round to three decimal places as​ needed.)

 

State the conclusion for the test.

1. Reject the null hypothesis. There is not sufficient evidence to support the claim that the cans of diet soda have mean weights that are lower than the mean weight for the regular soda. 
2. Fail to reject the null hypothesis. There is not sufficient evidence to support the claim that the cans of diet soda have mean weights that are lower than the mean weight for the regular soda.
3. Reject the null hypothesis. There is sufficient evidence to support the claim that the cans of diet soda have mean weights that are lower than the mean weight for the regular soda.
4. Fail to reject the null hypothesis. There is 
   sufficient evidence to support the claim that the cans of diet soda have mean weights that are lower than the mean weight for the regular soda.

 

b. Construct a confidence interval appropriate for the hypothesis test in part​ (a).

________________________________ ​(Round to three decimal places as​ needed.)

 

Does the confidence interval support the conclusion found with the hypothesis​ test?
______  because the confidence interval contains only negative values. 

 

5. Suppose 234 subjects are treated with a drug that is used to treat pain and 50 of them developed nausea. Use a 0.10 significance level to test the claim that more than 20
​% of users develop nausea.

Identify the null and alternative hypotheses for this test. Choose the correct answer below.

Identify the test statistic for this hypothesis test.

The test statistic for this hypothesis test is ______.  (Round to two decimal places as​ needed.)

Identify the​ P-value for this hypothesis test.

The​ P-value for this hypothesis test is ______. ​(Round to three decimal places as​ needed.)

Identify the conclusion for this hypothesis test.

1. Reject
   $H_0$

   There is ufficient evidence to warrant support of the claim that more than 20​% of users develop nausea.

2. Reject
   $H_0$

   There is not sufficient evidence to warrant support of the claim that more than 20​%  of users develop nausea.

3. Fail to reject
   $H_0$

   There is not sufficient evidence to warrant support of the claim that more than 20​% of users develop nausea. 

4. Fail to reject
   $H_0$

   . There is sufficient evidence to warrant support of the claim that more than 20% of users develop nausea.

 

6.  Suppose a mutual fund qualifies as having moderate risk if the standard deviation of its monthly rate of return is less than 6​%.  A​ mutual-fund rating agency randomly selects 28 months and determines the rate of return for a certain fund. The standard deviation of the rate of return is computed to be 4.11 ​%. 
Is there sufficient evidence to conclude that the fund has moderate risk at the

$\alpha =0.10$

equals 0.10 level of​ significance? A normal probability plot indicates that the monthly rates of return are normally distributed.

What are the correct hypotheses for this​ test?

The null hypothesis is H0​:  ____________

The alternative hypothesis is H1​: _______

 

Calculate the value of the test statistic.

${\chi }^2 =$

____. ​(Round to three decimal places as​ needed.)

Use technology to determine the​ P-value for the test statistic.

The​ P-value is ______.  ​(Round to three decimal places as​ needed.)

What is the correct conclusion at the

$\alpha =0.10$

level of​ significance?

Since the​ P-value is ____ than the level of​ significance, ____ the null hypothesis. There ___ sufficient evidence to conclude that the fund has moderate risk at the 0.10 level of significance.

 

7.  Suppose that in a random selection of 100 colored​ candies, 21​% of them are blue. The candy company claims that the percentage of blue candies is equal to 29​%. 
Use a 0.10 significance level to test that claim.

Identify the null and alternative hypotheses for this test. Choose the correct answer below.

Identify the test statistic for this hypothesis test.

The test statistic for this hypothesis test is _______.  (Round to two decimal places as​ needed.)

Identify the​ P-value for this hypothesis test.

The​ P-value for this hypothesis test is _______. ​(Round to three decimal places as​ needed.)

Identify the conclusion for this hypothesis test.

1. Reject
   $H_0$

   .   There is not sufficient evidence to warrant rejection of the claim that the percentage of blue candies is equal to 29​%

2. Fail to reject
   $H_0$

   .  There is not sufficient evidence to warrant rejection of the claim that the percentage of blue candies is equal to 29​%

3. Reject
   $H_0$

   .  There is sufficient evidence to warrant rejection of the claim that the percentage of blue candies is equal to 29​%.

4. Fail to reject
   $H_0$

   .  There is sufficient evidence to warrant rejection of the claim that the percentage of blue candies is equal to 29​%

 

8.  The test statistic of z= 1.29 is obtained when testing the claim that p > 0.9. 

a. Identify the hypothesis test as being​ two-tailed, left-tailed, or​ right-tailed.
b. Find the​ P-value.
c. Using a significance level of

$\alpha$

=0.01, should we reject

$H_0$

or should we fail to reject

$H_0$

​?

a. This is a _____________test.

b.​ P-value = ______ ​(Round to three decimal places as​ needed.)

c. Choose the correct conclusion below.

1. Reject
   $H_0$

   .  There is not sufficient evidence to support the claim that p > 0.9

2. Fail to reject
   $H_0$

   .  There is not sufficient evidence to support the claim that p > 0.9

3. Fail to reject 
   $H_{0.}$

   There is sufficient evidence to support the claim that p > 0.9

4. Reject
   $H_0$

   .  There is sufficient evidence to support the claim that p > 0.9.

 

9.  A simple random sample of pulse rates of 30 women from a normally distributed population results in a standard deviation of 10.9 beats per minute. The normal range of pulse rates of adults is typically given as 60 to 100 beats per minute. If the range rule of thumb is applied to that normal​ range, the result is a standard deviation of 10 beats per minute. Use the sample results with a 0.10 significance level to test the claim that pulse rates of women have a standard deviation equal to 10 beats per minute. Complete parts​ (a) through​ (d) below.

a. Identify the null and alternative hypotheses. Choose the correct answer below.

b. Compute the test statistic.

$x^2 =$

______ ​(Round to three decimal places as​ needed.)

c. Find the​ P-value of the test statistic.

The​ P-value of the test statistic is _______. ​(Round to three decimal places as​ needed.)

d. State the conclusion.

_________

$H_0.$

There ________ sufficient evidence to warrant rejection of the claim that pulse rates of women have a standard deviation equal to 10 beats per minute.

 

 

10.   Test the given claim. Identify the null​ hypothesis, alternative​ hypothesis, test​ statistic, P-value, and then state the conclusion about the null​ hypothesis, as well as the final conclusion that addresses the original claim. Among 2122 passenger cars in a particular​ region, 239 had only rear license plates. Among 329 commercial​ trucks, 47 had only rear license plates. A reasonable hypothesis is that commercial trucks owners violate laws requiring front license plates at a higher rate than owners of passenger cars. Use a 0.10 significance level to test that hypothesis.
a. Test the claim using a hypothesis test.
b. Test the claim by constructing an appropriate confidence interval.

a. Identify the null and alternative hypotheses for this test. Let population 1 correspond to the passenger cars and population 2 correspond to the commercial trucks.  Let a success be a vehicle that only has a rear license plate.

Identify the test statistic.  _____ ​(Round to two decimal places as​ needed.)

Identify the​ P-value. _______ (Round to three decimal places as​ needed.)

State the conclusion about the null​ hypothesis, as well as the final conclusion that addresses the original claim.

Reject

$H_0$

.  There is sufficient evidence to support the claim that commercial trucks owners violate laws requiring front license plates at a higher rate than owners of passenger cars.

Fail to reject

$H_0$

.  There is not sufficient evidence to support the claim that commercial trucks owners violate laws requiring front license plates at a higher rate than owners of passenger cars.

Reject

$H_0$

.  There is not sufficient evidence to support the claim that commercial trucks owners violate laws requiring front license plates at a higher rate than owners of passenger cars.

Fail to reject

$H_0$

.  There is sufficient evidence to support the claim that commercial trucks owners violate laws requiring front license plates at a higher rate than owners of passenger cars.

b. Identify the confidence interval limits for the appropriate confidence interval. Let population 1 correspond to the passenger cars and population 2 correspond to the commercial trucks.  Let a success be a vehicle that only has a rear license plate.

 

_________________ ​(Round to four decimal places as​ needed.)

Because the confidence interval limits  ________ ​0, there ____ a significant difference between the two proportions. There ____ sufficient evidence to support the claim that commercial trucks owners violate laws requiring front license plates at a higher rate than owners of passenger cars.