Week 4 Homework Assignment

 

1.  Is there a relation between the age difference between​ husband/wives and the percent of a country that is​ literate? Researchers found the​ least-squares regression between age difference​ (husband age minus wife​ age), y, and literacy rate​ (percent of the population that is​ literate), x, is 

$\hat{y}=–0.0542x+8.4$

. The model applied for

$17\le x\le 100.$

x. Complete parts​ (a) through​ (e) below.

​(a) Interpret the slope. Select the correct choice below and fill in the answer box to complete your choice.

For every unit increase in ________, the __________falls by  ____  units, on average.  ​(Type an integer or decimal. Do not​ round.)

​(b) Does it make sense to interpret the​ y-intercept? Explain. Choose the correct answer below.

Yes it makes sense to interpret the​ y-intercept because an​ x-value of 0 is within the realm of possibilities.

No it does not make sense to interpret the​ y-intercept because a​ y-value of 0 is impossible.

No it does not make sense to interpret the​ y-intercept because an​ x-value of 0 is impossible.

No it does not make sense to interpret the​ y-intercept because an​ x-value of 0 is outside the scope of the model.

No it does not make sense to interpret the​ y-intercept because a​ y-value of 0 is outside the scope of the model.

​(c) Predict the age difference between​ husband/wife in a country where the literacy rate is  percent.
  
______ years  ​(Round to one decimal place as​ needed.)

​(d) Would it make sense to use this model to predict the age difference between​ husband/wife in a country where the literacy rate is ​%?

No it does not make sense because an​ x-value of  is outside the scope of the model.

No it does not make sense because a​ y-value of  is outside the scope of the model.

Yes it makes sense because a​ y-value of  is within the realm of possibilities and within the scope of the model.

Yes it makes sense because an​ x-value of  is within the realm of possibilities and within the scope of the model.

​(e) The literacy rate in a country is 98 ​% and the age difference between husbands and wives is 2 years. Is this age difference above or below the average age difference among all countries whose literacy rate is 98 ​%? Select the correct choice below and fill in the answer box to complete your choice.
​(Round to one decimal place as​ needed.)

Below the average age difference among all countries whose literacy rate is 98 % is ___ years

Above the average age difference among all countries whose literacy rate is 98​% is ___ years
  

 

 

2.  The data below represent commute times​ (in minutes) and scores on a​ well-being survey. Complete parts​ (a) through​ (d) below.

​(a) Find the​ least-squares regression line treating the commute​ time, x, as the explanatory variable and the index​ score, y, as the response variable.
  

$\hat{y} = \_\_\_\_\_ x + \left(\_\_\_\_\right)$

  
​(Round to three decimal places as​ needed.)

​(b) Interpret the slope and​ y-intercept, if appropriate. Interpret the slope. Select the correct choice below​ and, if​ necessary, fill in the answer box to complete your choice.

For an index score of​ zero, the commute time is predicted to be ___ minutes .  ​(Round to three decimal places as​ needed.)

For a commute time of zero​ minutes, the index score is predicted to be ____ ​(Round to three decimal places as​ needed.)

For every unit increase in index​ score, the commute time falls by ___, on average.  ​(Round to three decimal places as​ needed.)

For every unit increase in commute​ time, the index score falls  by _____, 0.063​, on average.  ​(Round to three decimal places as​ needed.)

It is not appropriate to interpret the slope.

Interpret the​ y-intercept. Select the correct choice below​ and, if​ necessary, fill in the answer box to complete your choice.

For every unit increase in index​ score, the commute time  by ____, on average.   ​(Round to three decimal places as​ needed.)

For a commute time of zero​ minutes, the index score is predicted to be _____.  ​(Round to three decimal places as​ needed.)

For an index score of​ zero, the commute time is predicted to be _____minutes.  ​(Round to three decimal places as​ needed.)

For every unit increase in commute​ time, the index score falls  by _____ on average.  (Round to three decimal places as​ needed.)

It is not appropriate to interpret the​ y-intercept because a commute time of zero minutes does not make sense and the value of zero minutes is much smaller than those observed in the data set.

​(c) Predict the​ well-being index of a person whose commute time is 25 minutes.

The predicted index score is ______ ​(Round to one decimal place as​ needed.)

​(d) Suppose Barbara has a 20 ​-minute commute and scores 67.0  on the survey. Is Barbara more​ “well-off” than the typical individual who has a 20​-minute ​commute? Select the correct choice below and fill in the answer box to complete your choice.  ​(Round to one decimal place as​ needed.)

​Yes, Barbara is more​ well-off because the typical individual who has a ​20-minute commute scores ____

​No, Barbara is less​ well-off because the typical individual who has a ​20-minute commute scores ____

 

 

3.  A pediatrician wants to determine the relation that exists between a​ child’s height,​ x, and head​ circumference, y. She randomly selects 11 children from her​ practice, measures their heights and head​ circumferences, and obtains the accompanying data. Complete parts​ (a) through​ (g) below.

 

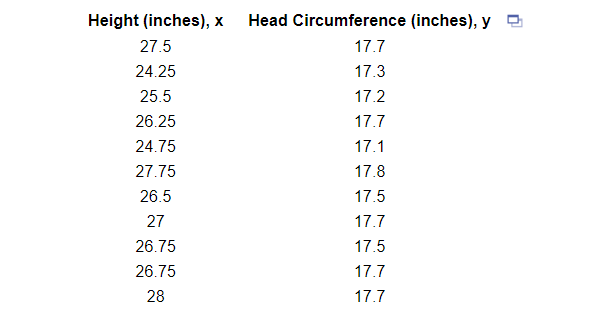
​(a) Find the​ least-squares regression line treating height as the explanatory variable and head circumference as the response variable.

$\hat{y}=\_\_\_\_ x +(\hspace{0.17em}\_\_\_)$

  
  
​(Round the slope to three decimal places and round the constant to one decimal place as​ needed.)

 

​(b) Interpret the slope and​ y-intercept, if appropriate.

First interpret the slope. Select the correct choice below​ and, if​ necessary, fill in the answer box to complete your choice.

For a height of 0​ inches, the head circumference is predicted to be ___ ​(Round to three decimal places as​ needed.)

For every inch increase in​ height, the head circumference increases by _____ in., on average.  (Round to three decimal places as​ needed.)

For a head circumference of 0​ inches, the height is predicted to be ____ in.  ​(Round to three decimal places as​ needed.)

For every inch increase in head​ circumference, the height increases  by  ____ in. on average.  (Round to three decimal places as​ needed.)

It is not appropriate to interpret the slope.

Interpret the​ y-intercept, if appropriate. Select the correct choice below​ and, if​ necessary, fill in the answer box to complete your choice.

For a head circumference of 0​ inches, the height is predicted to be ____ in.  ​(Round to one decimal place as​ needed.)

For every inch increase in head​ circumference, the height increased by ____ ​in., on average.  (Round to one decimal place as​ needed.)

For every inch increase in​ height, the head circumference increases  by ____ ​in., on average.  (Round to one decimal place as​ needed.)

For a height of 0​ inches, the head circumference is predicted to be ___ in.  (Round to one decimal place as​ needed.)

It is not appropriate to interpret the​ y-intercept.

​(c) Use the regression equation to predict the head circumference of a child who is 24.75 inches tall.

$\hat{y}=\_\_\_\_ in$

  
​(Round to two decimal places as​ needed.)

​(d) Compute the residual based on the observed head circumference of the 24.75 ​-inch-tall child in the table. Is the head circumference of this child above or below the value predicted by the regression​ model?

The residual for this observation is ____, meaning that the head circumference of this child is ____ the value predicted by the regression model.  ​(Round to two decimal places as​ needed.)

​(e) Draw the​ least-squares regression line on the scatter diagram of the data and label the residual from part​ (d). Choose the correct graph below.

 

(f) Notice that two children are 26.75  inches tall. One has a head circumference of 17.5  ​inches; the other has a head circumference of  17.7 inches. How can this​ be?

For children with a height of 26.75 ​inches, head circumferences vary.

The only explanation is that the difference was caused by measurement error.

The only explanation is that the difference is due to the fact that one observation was of a​ boy, and one observation was of a girl.

There is no logical explanation for thisthe two observations in question should have had the same head circumference.

​(g) Would it be reasonable to use the​ least-squares regression line to predict the head circumference of a child who was 32 inches​ tall? Why?

Nothis height is not possible.

Yesthis height is possible and within the scope of the model.

Yesthe calculated model can be used for any​ child’s height.

Nothis height is outside the scope of the model.

More information regarding the child is necessary to make the decision.

 

 

4.   An engineer wants to determine how the weight of a​ gas-powered car,​ x, affects gas​ mileage, y. The accompanying data represent the weights of various domestic cars and their miles per gallon in the city for the most recent model year. Complete parts​ (a) through​ (d) below.

 

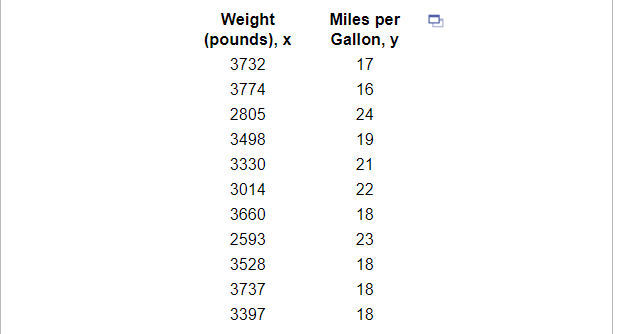
(a) Find the​ least-squares regression line treating weight as the explanatory variable and miles per gallon as the response variable.
  

$\hat{y}= \_\_\_\_x+\_\_\_$

  
​(Round the x coefficient to five decimal places as needed. Round the constant to two decimal places as​ needed.)

​(b) Interpret the slope and​ y-intercept, if appropriate. Choose the correct answer below and fill in any answer boxes in your choice.
​(Use the answer from part a to find this​ answer.)

A weightless car will get ____ enter your response here miles per​ gallon, on average. It is not appropriate to interpret the slope.

For every pound added to the weight of the​ car, gas mileage in the city will decrease by ___ mile(s) per​ gallon, on average. A weightless car will get __ miles per​ gallon, on average.

For every pound added to the weight of the​ car, gas mileage in the city will decrease by _____ ​mile(s) per​ gallon, on average. It is not appropriate to interpret the​ y-intercept.

It is not appropriate to interpret the slope or the​ y-intercept.

​(c) A certain​ gas-powered car weighs 3600  pounds and gets 20 miles per gallon. Is the miles per gallon of this car above average or below average for cars of this​ weight?

Below

Above

​(d) Would it be reasonable to use the​ least-squares regression line to predict the miles per gallon of a hybrid gas and electric​ car? Why or why​ not?

​No, because the hybrid is a different type of car.

​No, because the absolute value of the correlation coefficient is less than the critical value for a sample size of n11.

​Yes, because the hybrid is partially powered by gas.
.
​Yes, because the absolute value of the correlation coefficient is greater than the critical value for a sample size of n11.

 

5.  Because colas tend to replace healthier beverages and colas contain caffeine and phosphoric​ acid, researchers wanted to know whether cola consumption is associated with lower bone mineral density in women. The accompanying data lists the typical number of cans of cola consumed in a week and the femoral neck bone mineral density for a sample of 15 women. Complete parts​ (a) through​ (f) below.

 

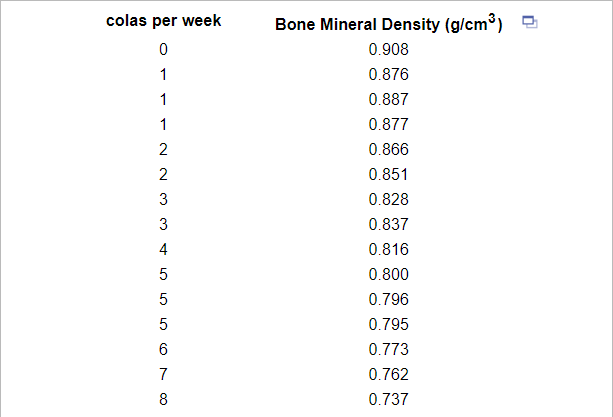
​(a) Find the​ least-squares regression line treating cola consumption per week as the explanatory variable.
  

$\hat{y}=\_\_\_\_x + ( )$

  
​(Round to three decimal places as​ needed.)

​(b) Interpret the slope. Select the correct choice below​ and, if​ necessary, fill in the answer box to complete your choice.

For every unit increase in bone​ density, the number of colas decreases by ___, on average.  ​(Round to three decimal places as​ needed.)

For 0 colas consumed in a​ week, the bone density is predicted to be ____ 

$g/c{m}^3$

​(Round to three decimal places as​ needed.)

For a bone density of 0 

$g/c{m}^3$

​, the number of colas consumed is predicted to be ____ ​(Round to three decimal places as​ needed.)

For every cola consumed per​ week, the bone density decreases by ____

$g/c{m}^3$

, on average  (Round to three decimal places as​ needed.)

It is not appropriate to interpret the slope.

 

​(c) Interpret the​ y-intercept. Select the correct choice below​ and, if​ necessary, fill in the answer box to complete your choice.

For every cola consumed per​ week, the bone density decreases by ___

$g/c{m}^3$

​, on average.  ​(Round to three decimal places as​ needed.)

For every unit increase in bone​ density, the number of colas decreases by ____, on average.  (Round to three decimal places as​ needed.)

For 0 colas consumed in a​ week, the bone density is predicted to be _____

$g/c{m}^3$

  (Round to three decimal places as​ needed.)

For a bone density of 0

$g/c{m}^3$

​, the number of colas consumed is predicted to be ____ in  (Round to three decimal places as​ needed.)

It is not appropriate to interpret the​ y-intercept.

​(d) Predict the bone mineral density of the femoral neck of a woman who consumes three colas per week.

$\hat{y}=\_\_\_\_ g/c{m}^3$

​(Round to three decimal places as​ needed.)

​(e) The researchers found a woman who consumed three colas per week to have a bone mineral density of 0.829 

$g/c{m}^3$

. Is this​ woman’s bone density above or below average among all women who consume three colas per​ week? 

This​ women’s bone density is ____ the average of ____

$g/c{m}^3$

(Round to three decimal places as​ needed.)

​(f) Would you recommend using the model found in part​ (a) to predict the bone mineral density of a woman who consumes two colas per​ day? Why? Select the correct choice below​ and, if​ necessary, fill in the answer box to complete your choice.

Yes —  an ​x-value that represents a woman consuming ____ colas per week is possible and within the scope of the model.  ​(Type an integer or a simplified​ fraction.)

No–an ​x-value that represents a woman consuming ____ colas per week is outside the scope of the model.  ​(Type an integer or a simplified​ fraction.)

Yes– the calculated model can be used for any number of colas consumed per week.

No– an ​x-value that represents a woman consuming ____ colas per week is not possible.  ​(Type an integer or a simplified​ fraction.)

More information regarding the woman is necessary to make the decision.

 

 

6.  The accompanying data represent the number of days​ absent, x, and the final exam​ score, y, for a sample of college students in a general education course at a large state university. Complete parts ​(a) through​ (e) below.

 

​(a) Find the​ least-squares regression line treating number of absences as the explanatory variable and the final exam score as the response variable.
  

$\hat{y}= \_\_\_\_\_x +$

_____(Round to three decimal places as​ needed.)

​(b) Interpret the slope and the​ y-intercept, if appropriate. Choose the correct answer below and fill in any answer boxes in your choice.   ​(Round to three decimal places as​ needed.)

The average final exam score of students who miss no classes is ___. It is not appropriate to interpret the slope.

For every additional​ absence, a​ student’s final exam score drops _____ ​points, on average. It is not appropriate to interpret the​ y-intercept.

For every additional​ absence, a​ student’s final exam score drops _____ points, on average. The average final exam score of students who miss no classes is ____

It is not appropriate to interpret the slope or the​ y-intercept.

 

(c) Predict the final exam score for a student who misses five class periods.

$\hat{y}=\_\_\_\_$

  (Round to two decimal places as​ needed.)

Compute the residual.
  
____  ​(Round to two decimal places as​ needed.)

Is the final exam score above or below average for this number of​ absences?

Below

Above

(d) Draw the​ least-squares regression line on the scatter diagram of the data. Choose the correct graph below.

 

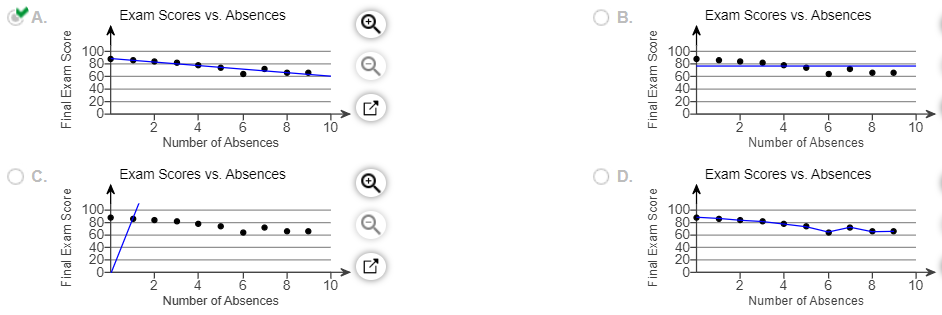
​(e) Would it be reasonable to use the​ least-squares regression line to predict the final exam score for a student who has missed 15 class​ periods? Why or why​ not?

​Yes, because the absolute value of the correlation coefficient is greater than the critical value for a sample size of n10.

​No, because the absolute value of the correlation coefficient is less than the critical value for a sample size of n10.

​Yes, because the purpose of finding the regression line is to make predictions outside the scope of the model.

​No, because 15 absences is outside the scope of the model.

 

 

 

7. The data in the table represent the number of licensed drivers in various age groups and the number of fatal accidents within the age group by gender. Complete parts ​(a) through ​(c) below.

 

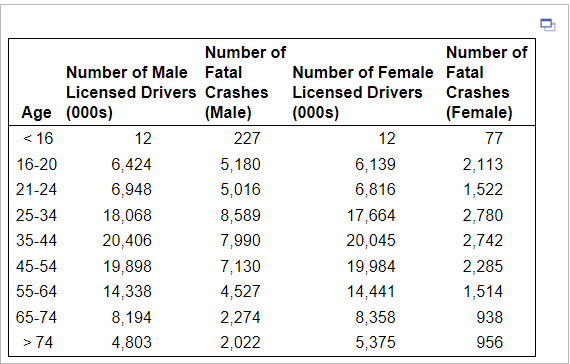
​(a) Find the​ least-squares regression line for males treating the number of licensed drivers as the explanatory​ variable, x, and the number of fatal​ crashes, y, as the response variable. Repeat this procedure for females.

Find the​ least-squares regression line for males.

$\hat{y}=\_\_\_\_ x + \_\_\_\_$

  ​(Round the x coefficient to three decimal places as needed. Round the constant to the nearest integer as​ needed.)

Find the​ least-squares regression line for females.

$\hat{y}=\_\_\_x + \_\_\_\_$

​(Round the x coefficient to three decimal places as needed. Round the constant to the nearest integer as​ needed.)

​(b) Interpret the slope of the​ least-squares regression line for each​ gender, if appropriate. How might an insurance company use this​ information?

What is the correct interpretation of the slope of the​ least-squares regression line for​ males? Select the correct choice below​ and, if​ necessary, fill in the answer box to complete your choice.  ​(Use the answer from part a to find this​ answer.)

If the number of fatal crashes increases by​ 1, then the number of male licensed drivers increases by ____ ​thousand, on average.

If the number of male licensed drivers increases by 1​ (thousand), then the number of fatal crashes increases by _____​, on average.

If the average age of all male licensed drivers increases by​ 1, then the number of fatal crashes increases by ____​, on average.

It does not make sense to interpret the slope.

 

What is the correct interpretation of the slope of the​ least-squares regression line for​ females? Select the correct choice below​ and, if​ necessary, fill in the answer box to complete your choice. ​(Use the answer from part a to find this​ answer.)

If the number of female licensed drivers increases by 1​ (thousand), then the number of fatal crashes increases by _____,  on average.

If the number of fatal crashes increases by​ 1, then the number of female licensed drivers increases by _____ thousand, on average.

If the average age of all female licensed drivers increases by​ 1, then the number of fatal crashes increases by _____​, on average.

It does not make sense to interpret the slope.

 

The slope of the regression line for males is _________ that for females. This means that males tend to be involved in ___________________   females. An insurance company may use this information to argue for _______________

(c) Was the number of fatal accidents for 16 to 20 year old males above or below​ average? Was the number of fatal accidents for 21 to 24 year old males above or below​ average? Was the number of fatal accidents for males greater than 74 years old above or below​ average? How might an insurance company use this​ information? Does the same relationship hold for​ females?

The number of fatal accidents for 16 to 20 year old males was ____________.
 The number of fatal accidents for 21 to 24 year old males was ____________ .
 The number of fatal accidents for males greater than 74 years old was ________ .

An insurance company could use it to argue for higher rates for _________ drivers and lower rates for ______ drivers.

Does the same relationship hold for​ females?
No
Yes

 

 

8.  Is the following a probability​ model? What do we call the outcome green?

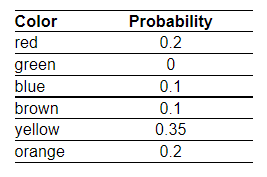
Is the table above an example of a probability​ model?

Yes, because the probabilities sum to 1 and they are all greater than or equal to 0 and less than or equal to 1

​No, because not all the probabilities are greater than 0.

No,  because the probabilities do not sum to 1  

Yes, because the probabilities sum to 1

What do we call the outcome  green?

Not so unusual event

Impossible event

Certain event

Unusual event

 

 

9.   Which of the following numbers could be the probability of an​ event?

​1 , -0.46, 0, 0.04, 1.41, 0.37

The numbers that could be a probability of an event are ___________

(Use a comma to separate answers as​ needed.)

 

 

10. Suppose you toss a coin 100 times and get 74  heads and 26 tails. Based on these​ results, what is the probability that the next flip results in a ​tail?

The probability that the next flip results in a tail is approximately ____ ​(Type an integer or decimal rounded to two decimal places as​ needed.)

 

11. According to a certain​ country’s department of​ education, 41.4​% of​ 3-year-olds are enrolled in day care. What is the probability that a randomly selected​ 3-year-old is enrolled in day​ care?

The probability that a randomly selected​ 3-year-old is enrolled in day care is _____ ​(Type an integer or a​ decimal.)

 

12.  A survey of  randomly selected high school students determined that 212 play organized sports. 
​(a) What is the probability that a randomly selected high school student plays organized​ sports?
​(b) Interpret this probability.

​(a) The probability that a randomly selected high school student plays organized sports is ____.  (Round to the nearest thousandth as​ needed.)

​(b) Choose the correct answer below.  ​(Type a whole​ number.)

If​ 1,000 high school students were​ sampled, it would be expected that exactly _____ of them play organized sports.

If​ 1,000 high school students were​ sampled, it would be expected that about _____ of them play organized sports.

 

 

13.   In a recent​ survey, it was found that the median income of families in country A was ​$57,300. What is the probability that a randomly selected family has an income  than ​$57,300​?

What is the probability that a randomly selected family has an income greater  than ​$57,300?
  

 

14   A golf ball is selected at random from a golf bag. If the golf bag contains 7green  ​balls, 6 black  ​balls, and 8 brown  ​balls, find the probability of the following event.
The golf ball is green or black .

The probability that the golf ball is green  or black  is  __________

 

15.  A golf ball is selected at random from a golf bag. If the golf bag contains 6  type A​ balls, 4 type B​ balls, and 3  type C​ balls, find the probability that the golf ball is not a type A ball.

The probability that the golf ball is not a type A ball is ______. ​(Type an integer or decimal rounded to three decimal places as​ needed.)

 

16  A standard deck of cards contains 52 cards. One card is selected from the deck.
​(a) Compute the probability of randomly selecting a diamond or heart

​(b) Compute the probability of randomly selecting a diamond, or heart, or club.

​(c)  Compute the probability of randomly selecting a ten or spade

(a)​ P(diamond or heart​) = ____ ​(Type an integer or a decimal rounded to three decimal places as​ needed.)

​(b)​ P(diamond or heart  or club ​) = ____ (Type an integer or a decimal rounded to three decimal places as​ needed.)

​(c)​ P(ten or spade​) = ___ ​(Type an integer or a decimal rounded to three decimal places as​ needed.)