Week 5 Homework Assignment

1.  A golf ball is selected at random from a golf bag. If the golf bag contains 5 black ​balls, 9 red ​balls, and 9 yellow ​balls, find the probability of the following event.
The golf ball is black  or red .

The probability that the golf ball is black or red  is

2.  A golf ball is selected at random from a golf bag. If the golf bag contains 6 type A​ balls, 4 type B​ balls, and 3 type C​ balls, find the probability that the golf ball is not a type A ball.

The probability that the golf ball is not a type A ball is _____

3.   A standard deck of cards contains 52 cards. One card is selected from the deck.
​(a) Compute the probability of randomly selecting a nine  or ace .
​(b) Compute the probability of randomly selecting a nine  or ace  or eight .
​(c) Compute the probability of randomly selecting an ace or diamond .

(a)​ P(nine or ace ​)
  

4.   According to a​ survey, the probability that a randomly selected worker primarily drives a van  to work is 0.825 . The probability that a randomly selected worker primarily

​(a) What is the probability that a randomly selected worker primarily drives a van or takes public transportation to​ work?

​P(worker drives a  or takes public transportation to ​work)  = _____

5.  The data in the table represent the number of drivers involved in fatal crashes in a certain region by day of the week and gender. Complete parts​ (a) through​ (e) below.

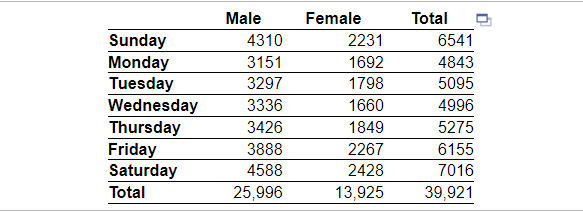
(a) Determine the probability that a randomly selected fatal crash involved a male

P(male) =

6.  About ​7% of the population of a large country is math phobic . If two people are randomly​ selected, what is the probability both are math phobic ​? What is the probability at least one is math phobic​? Assume the events are independent.

​(a) The probability that both will be math phobic is ______

7.   A test to determine whether a certain antibody is present is ​99.6% effective. This means that the test will accurately come back negative if the antibody is not present​ (in the test​ subject) 99.6​% of the time. The probability of a test coming back positive when the antibody is not present​ (a false​ positive) is 0.004. Suppose the test is given to four randomly selected people who do not have the antibody.
​(a) What is the probability that the test comes back negative for all four ​people?
​(b) What is the probability that the test comes back positive for at least one of the four ​people?

8.   Players in sports are said to have​ “hot streaks” and​ “cold streaks.” For​ example, a batter in baseball might be considered to be in a​ slump, or cold​ streak, if that player has made 10 outs in 10 consecutive​ at-bats. Suppose that a hitter successfully reaches base ​30% of the time he comes to the plate. Complete parts​ (a) through​ (c) below.

​(a) Find the probability that the hitter makes 10 outs in 10 consecutive​ at-bats, assuming​ at-bats are independent events.​ Hint: The hitter makes an out ​70% of the time.

P(hitter makes 10 consecutive outs) = ____

9.  Suppose Emerson loves 30​% of all bingo games .
​(a) What is the probability that Emerson loses two bingo games  in a​ row?
​(b) What is the probability that Emerson loses six bingo games in a​ row?
​(c) When events are​ independent, their complements are independent as well. Use this result to determine the probability that emerson loses six bingo games in a​ row, but   does not lose seven in a row.

a. The probability that Emerson loses two bingo game in a row is  _____

10.   According to a recent​ study, 8.8​% of high school dropouts are​ 16- to​ 17-year-olds. In​ addition, 5.7​% of high school dropouts are white​ 16- to​ 17-year-olds. What is the probability that a randomly selected dropout is​ white, given that he or she is 16 to 17 years​ old?

The probability that a randomly selected dropout is​ white, given that he or she is 16 to 17 years​ old, is  ______

11.   Suppose you just received a shipment of eight televisions. Two of the televisions are defective. If two televisions are randomly​ selected, compute the probability that both televisions work. What is the probability at least one of the two televisions does not​ work?

The probability that both televisions work is ______

12.