Exam2

1.  According to the report titled “Is the length of your arm related to your height?” students collected the data below. Let arm span be the explanatory variable

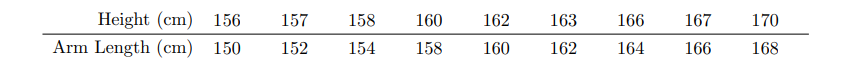
(a) (2 points) Describe the relationship between the data? Is the linear model appropriate? .

(b) (2 points) Interpret the slope of the regression line.

(c) (2 points) Interpret the y−intercept, if appropriate.

2  The Manua Loa Observatory, located on the island of Hawaii, has been monitoring carbon dioxide levels (CO2) levels in the atmoshpere since 1985. The table lists the average annual (CO2) levels measure in the parts per million (ppm) from 1990 to 2012. Note: The table lists the years since 1990 and corresponding CO2 level

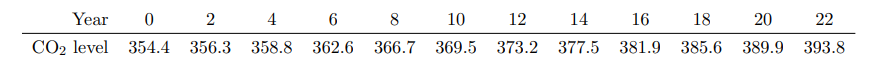
(a) (2 points) Find the coefficient of determination. What does the coefficient of determination say in this context?

(b) (3 points) Plot and sketch the residuals against the year and discuss whether the least square regression line is an appropriate model for the data, explain.

(c) (2 points) A friend wishes to predict the CO2 level this year (in 2020, 30 years after 1990). Find the predicted level of CO2. Is this estimate reliable? Explain.

3  (a) (3 points) Let the sample space be given by S = {Chris, Adam, Lida, Brian, Jose}. Suppose that the outcomes are equally likely.

i) Compute the probability of the event F = {Chris or Lida}.

ii) Find

(b) (9 points) The following data represent political party by age from a random sample of registered Iowa Voters.

Please write out the required probability statement as done in class and the fraction you use. Simplify to decimals where appropriate.

i) What is the probability that a randomly selected registered Iowa Voter is “30-44?”

ii) What is the probability that among “65+,” a randomly selected registered Iowa Voter is “Democrat?”

iii) What is the probability that among “Democrat,” a randomly selected registered Iowa Voter is “17-29?”

iv) Are the events is “Republican” and “30-44” independent? Explain. You must show at least two probabilities in your explanation.

4.   In a shipment of 12 4K ULTRA HD TV’s delivered to Best Buy it is known to the manufacturer that two of the televisions in the shipment are defective. The receiving company, Best Buy, will select two (2) televisions at random form the incoming shipment to inspect for defects.

Hint: You are selecting two televisions to inspect.

(a) (2 points) Determine the probability that both TV’s selected are not defective.

(b) (2 points) Determine the probability that both TV’s selected are defective.

(c) (3 points) Determine the probability that at least one TV is defected.

5. (8 points) A life insurance company sells a $250,000 1-year term life insurance policy to males.

i) Coverage for a 25-year-old male insurance costs $274.00. It is know that a healthy 25-year-old male has a death probability (probability of dying within one year) of 0.001602. Find the expected value of this policy to the insurance company and provide the probability distribution.

ii) Coverage for a 60-year-old male insurance costs $2,929.00. It is know that a healthy 60-year-old male has a death probability (probability of dying within one year) of 0.011533. Find the expected value of this policy to the insurance company and provide the probability distribution.

iii) If you were to recommend who sales personnel are supposed to focus on based on your work above, which age group would you direct insurance agents to target? Explain.

6.   Prescription opioids (drugs such as oxycodone, hydrocodone, fentanyl, morphine and codeine) are know to lead to illegal drug abuse. In 2019, the National Center for Health Statistics stated that it estimated estimated that 82% of people who abuse opiods started with (legal) prescription opioids. Suppose eight randomly selected opioids users (current addicts) are asked whether they started using opiods with (legal) prescription opiods. Let X be equal to the number of individuals who answer yes to
the question.

(a) (3 points) Explain as best as you can why this is a binomial experiment.

(b) (2 points) What is the probability that at least 4 people who abuse opiods started with (legal) prescription opioids.

(c) (3 points) Find the mean and standard deviation for this experiment, interpret the mean.