Section 2.6 Homework

1.   Consider the following equation. 

(a) Find y’  by implicit differentiation.

(b) Solve the equation explicitly for y and differentiate to get y’  in terms of x.

2. Find dy/dx  by implicit differentiation.

$x^2–4xy+y^2=4$

3.  Find dy/dx  by implicit differentiation.

$\frac{x^2}{x+y}=y^2+5$

4. Find dy/dx  by implicit differentiation.

$y \cos \left(x\right) =2x^2+5y^2$

5.  Find dy/dx  by implicit differentiation.

$\cos \left(xy\right)=1+\sin \left(y\right)$

6. Find dy/dx  by implicit differentiation.

$\sqrt{7xy}=6+x^{2}y$

7   Find dy/dx  by implicit differentiation.

$x \sin \left(y\right)+y \sin \left(x\right) =4$

8   Regard y as the independent variable and x as the dependent variable and use implicit differentiation to find dx/dy.

$x^5{y}^2–x^{5}y+5x{y}^3=0$

9.  Regard y as the independent variable and x as the dependent variable and use implicit differentiation to find dx/dy.

y sec(x) = 6x tan(y)

10.  Use implicit differentiation to find an equation of the tangent line to the curve at the given point.

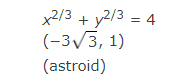
11.  Find y” by implicit differentiation.

$x^2+2y^2=2$

12. If 

find the value of y”’  at the point where x = 1.

Section 2.6 Homework Answers

12. If 

find the value of y”’  at the point where x = 1.

Answer: y”’= 42