Test 2

1.   Tanda teaches dance classes at Avocado Park High School under a grant from Los Angeles County. Her grant is up for review and she
wants to expand the classes so she can teach five days a week. She believes that her classes are beneficial to the students, so to
demonstrate this to the review board she randomly selects 2 of her dance students from EACH of her sessions over a week and asks them
how many of her sessions they attend each week and their GPA. Her results can be found in the Excel file “Test 2 Spring 2022.xlsx” on
Canvas. For the purpose of this test, use “Sessions” as the predictor and “GPA” as the response. Do NOT remove any outliers.

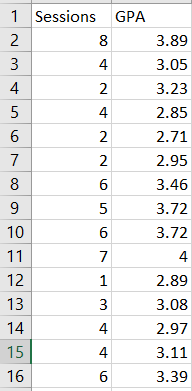
a. What population is Tanda studying here?
b. What method of sampling has Tanda employed?
c. Use the data from the file to create a scatterplot. Include the scatterplot in your document and describe its shape. What
kind of association do you see?
d. Compute and interpret the correlation coefficient.
e. Construct a linear model of the relationship between number of sessions attended and GPA.
f. Interpret the slope of the model in part e.
g. Interpret the initial value of the model you constructed in part e
h. use the linear model from part e to predict the GPA of a student who attends 4 of Tanda’s dance lessons in a week.
i. Use the linear model from part e to predict the GPA of a student who attends all 8 of Tanda’s sessions in a week.
j. If Tanda is able to expand her lessons to 10 sessions per week, what would the model predict for the GPA of a student
who attends all 10 sessions?
k. Bonus question: consider your answers to part j. What is wrong with this picture and why?
l. Based on your answers from parts d-i, do you think it would be reasonable for Tanda to conclude that attending more of
her dance sessions will increase a student’s GPA? Explain your thinking.

2. The goats of Avocado Park are becoming rather dapper. Currently, 47% of them wear an ascot regularly. Of the ascot-wearing goats, 65%
prefer the color blue. Of the non-ascot-wearing goats, 49% prefer the color blue. For convenience, I suggest you use event A to refer to
wearing an ascot and the event B to refer to preferring the color blue.
a. Create a decision tree to organize the sample space of the situation described in this problem.
b. Compute P(B), the probability that a random goat (ascot or no ascot) prefers the color blue.
c. Compute P(A|B), the probability that a random goat who PREFERS THE COLOR BLUE wears an ascot.

d. Bonus question: Compute the probability that a random goat who does not prefer the color blue wears an ascot.

3. Letitia’s next door neighbor Sarkis is buying gifts for his favorite goats. He’s heard about the ascot thing, so he figures that would be a
safe present. At the store he sees a box containing 15 ascots, so he grabs 7 of them to give to the goats. What he doesn’t notice is that 6
of the ascots are blue and the other 9 are gray.
a. How many different ways can he select the 7 ascots (ignore color for now)?
b. How many different ways could he select 4 blue and 3 gray ascots?
c. If he ignores color and just grabs 7 random ascots, what would be the probability that he grabs 4 blue and 3 gray
ascots?
d. Bonus question: What is the probability that less than 3 of the ascots Sarkis selects will be gray?

4. Hadey wants to give his mother Old Billie (both are goats) an ascot for her birthday (which she seems to have every month somehow), so
he warns his favorite store that he’ll need an ascot in two weeks. They order 12 since they seem to be a hot item, but they don’t pay attention
to color either. Hadey only needs one blue ascot for his mother, but each ascot has only a 25% chance of being blue. Assume that the colors
of the 12 ascots are independent.

a. What is the probability that all 12 of the ascots are blue?

b. What is the probability that NONE of the 12 ascots are blue?
c. What is the probability that AT LEAST ONE of the 12ascots is blue?

Test 2 Answers

  Tanda teaches dance classes at Avocado Park High School under a grant from Los Angeles County. Her grant is up for review and she
wants to expand the classes so she can teach five days a week. She believes that her classes are beneficial to the students, so to
demonstrate this to the review board she randomly selects 2 of her dance students from EACH of her sessions over a week and asks them
how many of her sessions they attend each week and their GPA