Week 6 Homework Assignment

 

1. Determine whether the following graph can represent a normal density function.

 

Could the graph represent a normal density​ function?

 

 

2.  The graph of a normal curve is given. Use the graph to identify the value of

$\mu$

 and

$\sigma$

.

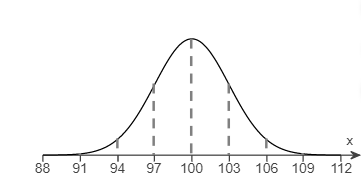
The value of 

$\mu$

is 

The value of 

$\sigma$

  is

 

3.  Determine the area under the standard normal curve that lies to the right of (a) Z = -0.13, (b) Z = -0.83, (c) Z = -0.93, and (d) Z = 0.69

 

​(a) The area to the right of Z = -0.13 is____
  
(b) The area to the right of Z = – 0.83 is _____
  
​(c) The area to the right of Z = -0.93 is _____

(d) The area to the right of Z = 0.69 is _____

 

 

4  Determine the area under the standard normal curve that lies between (a) Z = -0.86 and Z = 0.86, (b) Z = -2.72, and (c) Z = -2.07 and Z= 0-0.79

 

​(a) The area to the right of Z = -0.86 and Z=0.86  is____
  
(b) The area to the right of Z = – 2.72 and Z = 0 is _____
  
​(c) The area to the right of Z = -2.07 and Z = -0.79 is _____

 

 

5.  Determine the total area under the standard normal curve in parts ​(a) through ​(c) below.

(a) Find the area under the normal curve to the left of z = -1 plus the area under the normal curve to the right of z = 1

The combined area is  ______

 

(b) Find the area under the normal curve to the left of z = -1.53 plus the area under the normal curve to the right of z=2.53.

The combined area is 

 

(c) Find the area under the normal curve to the left of z = -0.22 plus the area under the normal curve to the right of z=1.40.

The combined area is 
  

 

6.   Find the​ z-score such that the area under the standard normal curve to the left is 0.97.

  
1.88 is the​ z-score such that the area under the curve to the left is 0.97 .
​(Round to two decimal places as​ needed.)

 

7.  Find the​ z-score such that the area under the standard normal curve to the right is 0.29.

The approximate​ z-score that corresponds to a right tail area of 0.29 is _____   (Round to two decimal places as​ needed.)

 

8.   Find the​ z-scores that separate the middle ​42% of the distribution from the area in the tails of the standard normal distribution.

The​ z-scores are ______   ​(Use a comma to separate answers as needed. Round to two decimal places as​ needed.)

 

9. Assume the random variable X is normally distributed with mean =50  and standard deviation =7. Compute the probability. Be sure to draw a normal curve with the area corresponding to the probability shaded

P(X>36)

Which of the following normal curves corresponds to  P(X>36).

P(X>36) = _____

 

10  Assume that the random variable X is normally​ distributed, with mean =55 and standard deviation =11 . Compute the probability. Be sure to draw a normal curve with the area corresponding to the probability shaded.

P(X

$\le$

48)
Which of the following shaded regions corresponds to  P(X

$\le$

48)

 

P(X

$\le$

48)  = ____

 

 

11  Assume the random variable X is normally distributed with mean =50  and standard deviation =7 . Compute the probability. Be sure to draw a normal curve with the area corresponding to the probability shaded.

P(35<x<58)

Which of the following normal curves corresponds to P(35<X<58) ​?

 

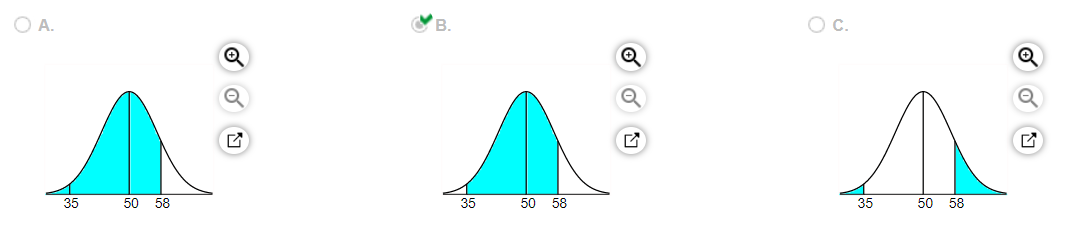
P(35<x<58) = ____

 

12.  Assume the random variable X is normally distributed with mean =50 and standard deviation =7 . Compute the probability. Be sure to draw a normal curve with the area corresponding to the probability shaded.

$P(57\le X\le 68)$

Which of the following normal curves corresponds to ​

$P (57\le X\le 68)$

 

$P(57\le X\le 68)$

= ____

 

 

 

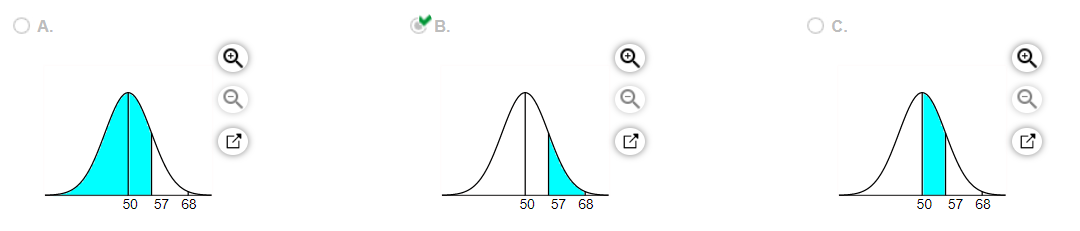
13.  Assume that the random variable X is normally​ distributed, with mean 45 and standard deviation =10 . Compute the probability ​

$P(38<X\le 55)$

. Be sure to draw a normal curve with the area corresponding to the probability shaded.

Draw a normal curve with the area corresponding to the probability shaded. Choose the correct graph below.

$P(38<X\le 55)$

= _____

 

 

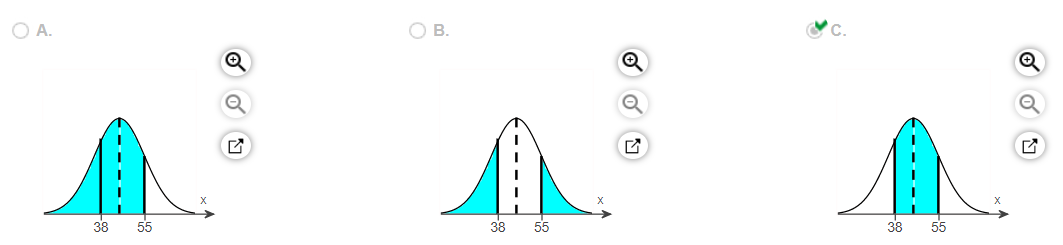
14. Assume the random variable X is normally distributed with mean 50  and standard deviation 7. Find the  77th percentile.

 

The 77th percentile is ______________

 

 

15. The mean incubation time for a type of fertilized egg kept at a certain temperature is 17 days. Suppose that the incubation times are approximately normally distributed with a standard deviation of 1 day  . Complete parts​ (a) through​ (e) below.

 

​(b) Find and interpret the probability that a randomly selected fertilized egg hatches in less than 15 days.
The probability that a randomly selected fertilized egg hatches in less than  days is _____

 

Interpret this probability. Select the correct choice below and fill in the answer box to complete your choice.  ​(Round to the nearest integer as​ needed.)

If 100 fertilized eggs were randomly​ selected, exactly ____ would be expected to hatch on day 15 .

If 100 fertilized eggs were randomly​ selected, __ of them would be expected to hatch in less than 15  days.

In every group of 100 fertilized​ eggs, __  eggs would be expected to hatch  in less than 15 days.

​(c) Find and interpret the probability that a randomly selected fertilized egg takes over 19 days to hatch.

The probability that a randomly selected fertilized egg takes over 19 days to hatch is _____.  (Round to four decimal places as​ needed.)

Interpret this probability. Select the correct choice below and fill in the answer box to complete your choice.  ​(Round to the nearest integer as​ needed.)

If 100 fertilized eggs were randomly​ selected, exactly  ____ would be expected to hatch on day 19.

If 100 fertilized eggs were randomly​ selected,  ___ of them would be expected to take more than 19 days to hatch.

In every group of 100 fertilized​ eggs,  ____ eggs would be expected to hatch in more than 19 days.

 

​(d) Find and interpret the probability that a randomly selected fertilized egg hatches between 16 and 17  days is _____

The probability that a randomly selected fertilized egg hatches between 16  and 17 days is _____ ​(Round to four decimal places as​ needed.)

 

Interpret this probability. Select the correct choice below and fill in the answer box to complete your choice. ​(Round to the nearest integer as​ needed.)

In every group of 100 fertilized​ eggs, ___ eggs would be expected to hatch between 16 and 17 days.

If 100 fertilized eggs were randomly​ selected, exactly ____ would be expected to hatch on day 16 or on day 17.

If 100 fertilized eggs were randomly​ selected, ___ of them would be expected to hatch between 16  and 17  days.

​(e) Would it be unusual for an egg to hatch in less than 14  ​days? Why?
The probability of an egg hatching in less than 14 days is  ______ so it _____ be unusual since the probability is ____ than 0.05
  

 

16. The number of chocolate chips in an​ 18-ounce bag of chocolate chip cookies is approximately normally distributed with a mean of 1252  chips and standard deviation 129  chips.
​(a) What is the probability that a randomly selected bag contains between 1000 and 1500  chocolate​ chips, inclusive? 
​(b) What is the probability that a randomly selected bag contains fewer than 1050 chocolate​ chips? 
​(c) What proportion of bags contains more than 1200 chocolate​ chips? 
​(d) What is the percentile rank of a bag that contains 1000  chocolate​ chips?

 

 

17.   A study found that the mean amount of time cars spent in​ drive-throughs of a certain​ fast-food restaurant was 158.2  seconds. Assuming​ drive-through times are normally distributed with a standard deviation of  ​33 seconds, complete parts​ (a) through​ (d) below.

​(a) What is the probability that a randomly selected car will get through the​ restaurant’s drive-through in less than 102  ​seconds?

​(b) What is the probability that a randomly selected car will spend more than  201 seconds in the​ restaurant’s drive-through?

​(c) What proportion of cars spend between 2 and 3 minutes in the​ restaurant’s drive-through?

​(d) Would it be unusual for a car to spend more than  3 minutes in the​ restaurant’s drive-through?​ Why?

 

 

18.  The lengths of a particular​ animal’s pregnancies are approximately normally​ distributed, with mean of 274 days and standard deviation 16  days.
​(a) What proportion of pregnancies lasts more than 294  ​days?
​(b) What proportion of pregnancies lasts between 254  and 286 ​days?
​(c) What is the probability that a randomly selected pregnancy lasts no more than  ​242 days?
​(d) A​ “very preterm” baby is one whose gestation period is less than 250  days. Are very preterm babies​ unusual?

 

 

19.   Suppose that the lifetimes of light bulbs are approximately normally​ distributed, with a mean of  57 hours and a standard deviation of 3.5  hours. With this​ information, answer the following questions.
​(a) What proportion of light bulbs will last more than 61 ​hours?
​(b) What proportion of light bulbs will last 52 hours or​ less?
​(c) What proportion of light bulbs will last between 59 and 62  ​hours?
​(d) What is the probability that a randomly selected light bulb lasts less than 45 ​hours?

 

 

20.  Steel rods are manufactured with a mean length of 29 centimeter​ (cm). Because of variability in the manufacturing​ process, the lengths of the rods are approximately normally distributed with a standard deviation of 0.08  cm. Complete parts ​(a) to ​(d).

​(a) What proportion of rods has a length less than 28.9  ​cm?
  
​(b) Any rods that are shorter than 28.81  cm or longer than 29.19 cm are discarded. What proportion of rods will be​ discarded?
  
​(c) Using the results of part ​(b)​, if 500 rods are manufactured in a​ day, how many should the plant manager expect to​ discard?
 
​(d) If an order comes in for 10,000 steel​ rods, how many rods should the plant manager expect to manufacture if the order states that all rods must be between 28.9 cm and 29.1 ​cm?
  

 

Week 6 Homework Assignment Answers