Test 3

1.  Hadey the goat is considering creating an independent movie studio for goat movies.  From his preliminary research he knows that the distribution of the variable G, the number of movies that a goat watches in a month, is as follows 

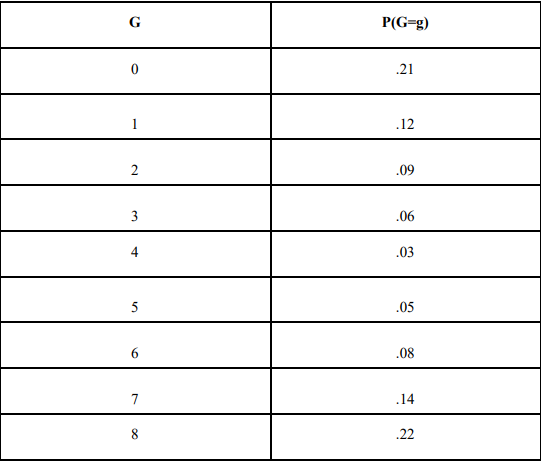
a. What is the mean of G?

b. What is the standard deviation of G?

c. What can you say about the shape of the distribution of G?

d. What is the probability that a randomly selected goat watches between 3 and 5 movies in a month (inclusive)?

e. If Hadey selects a random sample of 50 goats and asks them how many movies they have seen in a month, describe the distribution of 𝑔 , the mean number of
movies per goat that the goats in the sample watched in the past month.

f. What is the probability that a random sample of 50 goats watches a sample mean of between 3 and 5 movies per goat in a month? Use the distribution you
described in part d for your work.

2.   Hadey wants to know how big a market there is for goat moviesspecifically, so he collects a random sample of 120 residents of Avocado Park and asks them if they would like to watch a movie made by goats. In fact, 78% of the residents of Avocado Park would like to watch a movie made by goats.

a. For the sake of independence, how large would the population of Avocado Park need to be for a sample of this size?

b. Supposing Avocado Park is at least as large as the size you stated in part a, what would be the probability that more than 100 of the residents in the sample would
like to watch a movie made by goats?

c. Again supposing the population of Avocado Park is sufficiently large, what would be the probability that between 70 and 100 of those surveyed would like to
see a movie made by goats?

d. How many of those sample should be EXPECTED to like to watch a movie made by goats?

e. Consider the variable , the proportion of residents in the sample that would like to see a movie made by goats.

3.  Hadey’s secret weapon in developing his studio is movie length. He is convinced that the run time is the most important thing in a movie and he intends to bring shorter movies to market. To find the sweet spot, he collects a random sample of Avocado Park residents and asks them what they think the perfect movie length is. His results can be found in the Excel file “movie length.xlsx” on Canvas.

a. Is it safe to assume that the distribution of reported perfect movie lengths is normal? Explain.

b.  Is it safe to assume that the distribution of mean reported perfect movie lengths for samples of this size is normal? Explain.

4. Suppose that the distribution of preferred movie lengths is in fact uniformly distributed for Avocado Park residents between 30 and 350 minutes.

a. . Draw a graph of the distribution of preferred movie times. Don’t forget the density.

b. What is the probability that a random resident of Avocado Park prefers movies that are less than 60 minutes long?

c. What is the probability that a random resident of Avocado Park would prefer a movie to be between 60 and 120 minutes?

d. What is the probability that a random resident of Avocado Park would prefer a movie to be exactly 45 minutes?

e. What is the mean preferred movie length for residents of Avocado Park?

f. What is the standard deviation of preferred movie lengths for residents of Avocado Park?

g. Considering samples of size 43, describe the distribution of sample mean preferred runtimes

h. Bonus question: Should the sample from the data file in question 3 be considered to have an unusually low mean?

Test 3 Answers

1. 

a. What is the mean of G?

Answer:

E[G] = 0x0.21 + 1×0.12 + 2×0.09 + … + 8×0.22 = 4.07