Exam 2

1. Form a polynomial whose zeros and degree are given.
​Zeros: ​9, multiplicity​ 1; -4  ​, multiplicity​ 2;   degree 3

Type a polynomial with integer coefficients and a leading coefficient of 1 in the box below.

f(x) =

2.

$Analyze the polynomial function f\left(x\right) = (x+4) {(x–1)}^2 u\sin g parts \left(a\right) through \left(e\right).$

​(a) Determine the end behavior of the graph of the function.
​(b) Find the​ x- and​ y-intercepts of the graph of the function.

​(c) Determine the zeros of the function and their multiplicity. Use this information to determine whether the graph crosses or touches the​ x-axis at each​ x-intercept.
​(d) Determine the maximum number of turning points on the graph of the function.
(e) Use the above information to draw a complete graph of the function. Choose the correct graph below.

3. Use the graph shown to find the following.
​(a)  The domain and range of the function
​(b)  The​ intercepts, if any
​(c)  Horizontal​ asymptotes, if any
​(d)  Vertical​ asymptotes, if any
​(e)  Oblique​ asymptotes, if any

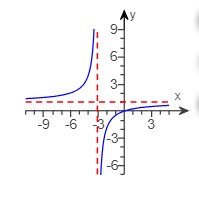
​(a)  What is the​ domain? Select the correct choice below and fill in any answer boxes within your choice.
What is the​ range? Select the correct choice below and fill in any answer boxes within your choice.
​(b)  Find the​ x-intercepts, if there are any. Select the correct choice below and fill in any answer boxes within your choice.
Find the​ y-intercepts, if there are any. Select the correct choice below and fill in any answer boxes within your choice.
(c)  Find the horizontal​ asymptotes, if there are any. Select the correct choice below and fill in any answer boxes within your choice.
Find the vertical​ asymptotes, if there are any. Select the correct choice below and fill in any answer boxes within your choice.
Find the oblique​ asymptotes, if there are any. Select the correct choice below and fill in any answer boxes within your choice.

4.  Solve the inequality algebraically.

List the intervals and sign in each interval. Complete the following table.

5. Solve the inequality algebraically.

$\frac{x+2}{x–9}<0$

6.

The remainder is

7.  Use the rational zeros theorem to find all the real zeros of the polynomial function. Use the zeros to factor f over the real numbers.

$f\left(x\right) = x^3+5x^2–73x–77$

Find the real zeros of f. Select the correct choice below​ and, if​ necessary, fill in the answer box to complete your answer.
Use the real zeros to factor f.

8. Form a polynomial​ f(x) with real coefficients having the given degree and zeros.
Degree​ 4;  ​ zeros: ​2, multiplicity​ 2; 3i

Enter the polynomial. Let a represent the leading coefficient.

9.  Use the given zero to find the remaining zeros of the function.

$f\left(x\right)=x^3–3x^2+4x–12; zero: –2i$

The remaining​ zero(s) of f​ is(are) 

10.   Solve the equation.

$4^{x^2–27}={16}^{3x}$

11. Use properties of logarithms to find the exact value of the expression.  Do not use a calculator.

${\log }_{7}4 . {\log }_{4}343$

12.  Write the expression as a sum​ and/or difference of logarithms. Express powers as factors.

$\ln \left(x^{12}\sqrt{2–x}\right), 0<x<2$