Introduction to Calculus
TOPIC ONE: POWER RULE
The power rule is the most basic concept of derivation and it is the most commonly used as well in Calculus. It’s actually one of the five basic differentiation rule that will come across as useful as you go on through harder concepts. This rule simply tells us that the derivative of a function raised to nth exponent is equals to the n exponent multiplied by the whole number raised to n-1. It is expressed as:
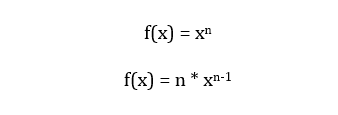
When and how to use it?
The power rule is simple and you can manipulate functions that usually use the quotient rule into simpler expression and use the power rule instead. In fact, its formal definition is the derivative of function x to the nth power is equal to n multiplied by function x raise to n minus one power. If you see an exponent in your function or whole expression, that’s the time that you will use power rule hence the name. Everything that is raised to nth power requires the method of power rule.
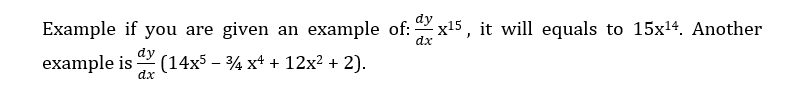
Don’t be discouraged about it’s seemingly long expression because for the whole equation, we will only need to use the power rule. Notice that it’s a simple addition and subtraction with only exponents with a constant last term which when we differentiate will equal to 0. So following the power rule, it will look like this:
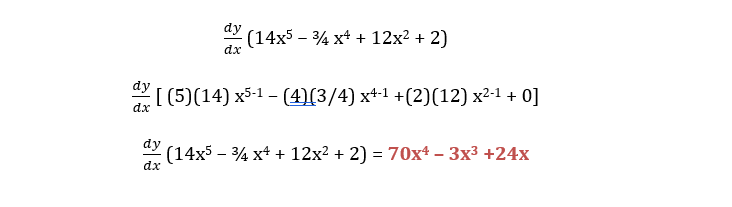
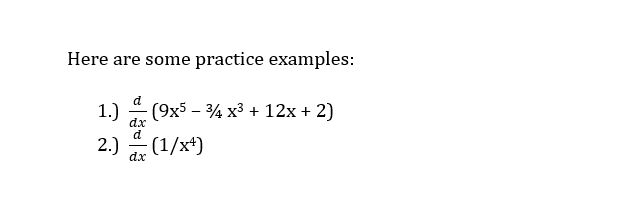
TOPIC TWO: PRODUCT RULE
The product rule is used when two functions are placed seemingly next to each other to differentiate its product hence: (fg)’= fg’ + gf’. In words, it can be read, as the derivative of fg is equal to f multiplied by the derivative of g plus g multiplied by the derivative of f where f is the first function and g is the second function. The letters are interchangeable since it’s addition and multiplication as long as you follow the concept, some references even use f and g as their variable while others us u and v.
When and how to use it?
The product rule is used when you need to find the derivative of the product of two functions.

In this case, we will be using the product rule where the first function f is x3 and the second function g is sin x. If you’re wondering why it isn’t read as one function, it’s because sin x is a trigonometric function while x3 is an algebraic function and they are beside each other, it’s no different when you see an equation that looks like (2)(x). So to use it, we must first identify the derivative of f which is 3x2 using the power rule where you multiply the exponent by the whole number, in this case one and subtract 1 from it’s exponent then the derivative of g which is cos x using the trigonometric identities.
It will look like this if we applied the product rule:
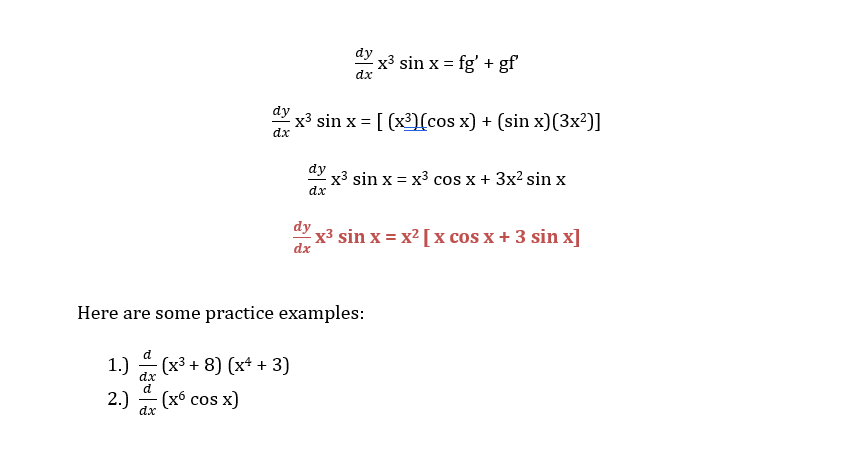
TOPIC THREE: QUOTIENT RULE
This is another one of the five basic differentiation rules. The quotient rule is a method used to find the derivative of a function that is expressed as a ratio or quotient of two functions. The quotient rule simply tells us that the function f prime of x is equal to u(x) which is the numerator and v(x) which is the denominator and to solve it you will get the derivative of u and multiply it with v plus derivative of v multiplied by u all over v(x)2. Once again, the multiplication of numbers’ order is interchangeable, as you still will come up with the same answers. Generally, the quotient rule will look like this:
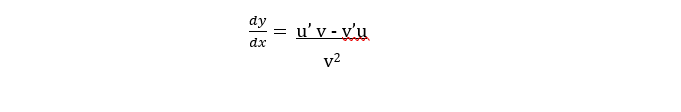
When and how to use it?
The quotient rule is applicable when you are deriving a fraction or ratio and therefore getting the quotient of it as the name implies. To use it, we will be applying the statement above: u prime multiplied by v plus v prime multiplied by u all over v2. So for example, we are given the function: x3/cos x. First thing to do is identify u which is the numerator x3 and its differentiation will equal to 3x2 following the power rule. Therefore v is the denominator cos x which when differentiated will equal to –sin x following the trigonometric identity.

TOPIC FOUR: CHAIN RULE
Moving onto the next lesson, the chain rule is fairly useful because you can use this rule to solve ratios that supposedly requires you to use the quotient rule. This is used to simplify the whole working equation so you would only need to use the power rule and the chain rule instead of the quotient rule. The chain rule states that the derivative of f (g(x))) is f prime (g(x)) multiplied by g prime of x. In order words, it can be used to differentiate composite functions such as sin (x2). It’s a technique to solve for derivatives that seems to look like it can be solved by a simple product or power rule. The chain rule from the name itself gets the partial derivatives of each function. Generally it looks like this in a mathematical equation:
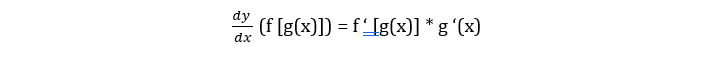
When and how to use it?
As stated, the chain rule is usually used when there is a composite function. The chain rule’s aim is to break down the calculation into a series of simpler steps. The first thing to do is identifying the outer function and the inner function.
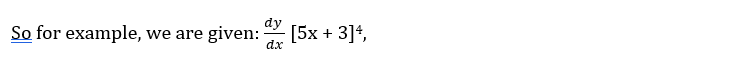
we can see from the exponent that we will be using the power rule for the whole equation, it is the outside function while the inside function g is 5x + 3. Deriving the inside function g’(x) will equal to 5x + 0 since 3 is a constant it will equal to zero. Now, following the formula:
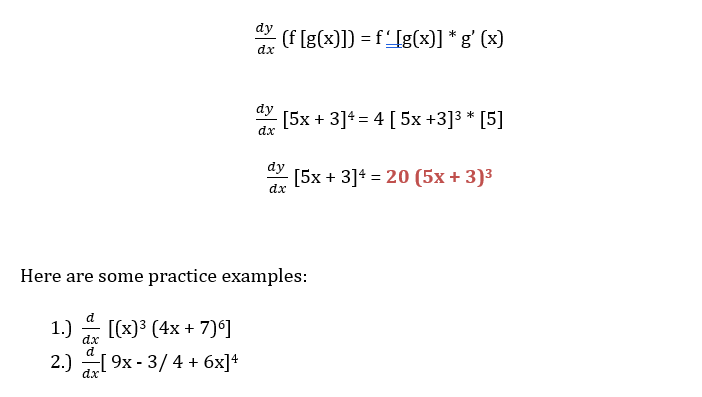
TOPIC FIVE: DERIVATIVES OF LOGARITHMIC FUNCTIONS
The differentiation of logarithmic functions are based on the chain rule but we also have to keep in mind their algebraic properties like to cancel ln, you will multiply both sides by e to further simplify the equation since the derivative of e is just eu multiplied by the derivative of u or it’s exponent. So listing down its derivatives, we have:
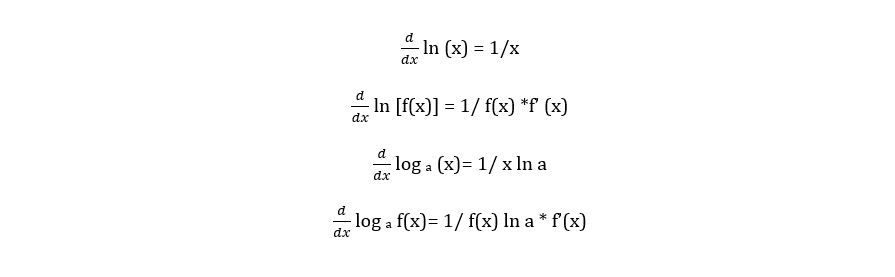
When and how to use it?
It’s easy identifying when these will be used, if you see ln or log, that will be the time to apply the formula stated above and it’s also easy applying them as long as you memorize the formulas. You will simply copy the format how the formula is written and employ the appropriate one for your equation. The logarithmic functions may seem intimidating but understanding its concept it’s quite simple. For example, the derivative of ln x is 1/x because ln naturally results to a fraction with the variable next to it being the denominator. For log, it’s also a fraction with ln and its base a because of its mathematical properties. The rest seems like chain rule- breaking down the complex into a series of simpler equations. For example, we are given: ln ( sin x), following the formula above, it will simply equal to cot x because u prime or the derivative of sin x is cos x there du/ u = cos x/ sin x and following the trigonometric identity, cos x/ sin x is cot x.

How We Safeguard Your Tutor Quality
All tutors are required to have relevant training and expertise in their specific fields before they are hired. Only qualified and experienced tutors can join our team
All tutors must pass our lengthy tests and complete intensive interview and selection process before they are accepted in our team
Prior to assisting our clients, tutors must complete comprehensive trainings and seminars to ensure they can adequately perform their functions
Interested in becoming a tutor with Online Class Ready?
Share your knowledge and make money doing it
1. Be your own boss
2. Work from home
3. Set your own schedule


