Section 1.5 Homework

 

1.  Use the given graph of f to state the value of each quantity, if it exists. (If an answer does not exist, enter DNE.)

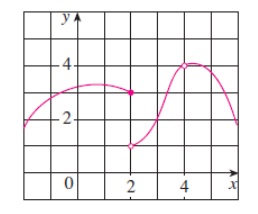
a.

$\underset{x\to 2^{–}}{\lim }f\left(x\right)$

 

b.

$\underset{x\to 2^{+}}{\lim }f\left(x\right)$

 

c.

$\underset{x\to 2}{\lim }\left(f\right(x)$

 

d. f(2)

 

e.

$\underset{x\to 4}{\lim }f\left(x\right)$

 

f. f(4)

 

2.  For the function h whose graph is given, state the value of each quantity, if it exists. (If an answer does not exist, enter DNE.)

a.

$\underset{x\to –3^{–}}{\lim }h\left(x\right)$

 

b.

$\underset{x\to –3^{+}}{\lim }h\left(x\right)$

 

c. 

$\underset{x\to –3}{\lim }h\left(x\right)$

 

d. h(-3)

 

e.

$\underset{x\to 0^{–}}{\lim }h\left(x\right)$

 

f.

$\underset{x\to 0^{+}}{\lim }h\left(x\right)$

 

g. 

$\underset{x\to 0}{\lim }h\left(x\right)$

 

h.  h(0)

 

i

$\underset{x\to 2}{\lim }h\left(x\right)$

 

j. h(2)

 

k. 

$\underset{x\to 5^{+}}{\lim }h\left(x\right)$

 

l.

$\underset{x\to 5^{–}}{\lim }h\left(x\right)$

 

 

 

3. For the function g whose graph is given, state the value of each quantity, if it exists. (If an answer does not exist, enter DNE.)

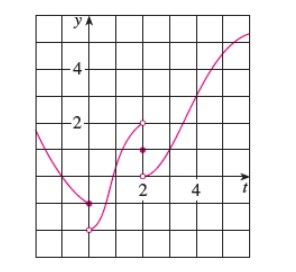
a.

$\underset{t\to 0^{–}}{\lim }g\left(t\right)$

 

b. 

$\underset{t\to 0^{+}}{\lim }g\left(t\right)$

 

c.

$\underset{t\to 0}{\lim }g\left(t\right)$

 

d. 

$\underset{t\to 2^{–}}{\lim }g\left(t\right)$

 

e.

$\underset{t\to 2^{+}}{\lim }g\left(t\right)$

 

f.

$\underset{t\to 2}{\lim }g\left(t\right)$

 

g. g(2)

 

h.

$\underset{t\to 4}{\lim }g\left(t\right)$

 

 

4. For the function f whose graph is shown, state the following. (If an answer does not exist, enter DNE.)

 

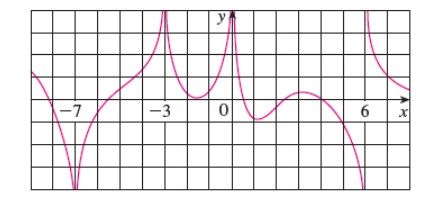
a.

$\underset{x\to –7}{\lim }f\left(x\right)$

 

b. 

$\underset{x\to –3}{\lim }f\left(x\right)$

 

c.

$\underset{x\to 0}{\lim }f\left(x\right)$

 

d.

$\underset{x\to 6^{–}}{\lim }f\left(x\right)$

 

e.

$\underset{x\to 6^{+}}{\lim }f\left(x\right)$

 

f.  The equations of the vertical asumptotes

x=                      (smallest value)

x=

x=

x=                       (largest value)

 

 

5.Sketch the graph of the function.

 

 

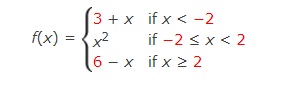
Use the graph to determine the values of a for which 

$\underset{x\to a}{\lim }f\left(x\right)$

  does not exist.  (Enter your answers as a comma-separated list.)

 

 

6. Sketch the graph of an example of a function f that satisfies all of the given conditions.

 

 

 

 

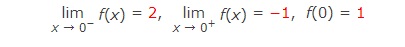
7. Sketch the graph of an example of a function f that satisfies all of the given conditions.

 

 

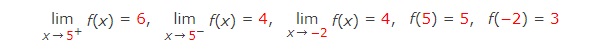
8. Determine the infinite limit.

$\underset{x\to 6^{+}}{\lim }\frac{x+7}{x–6}$

 

9. Determine the infinite limit

$\underset{x\to 9}{\lim }\frac{8–x}{{(x–9)}^2}$

 

 

10  Determine the infinite limit.

$\underset{x\to {(\mathrm{\pi }/2)}^{+}}{\lim }\frac{4}{x}sec\left(x\right)$

 

11.  Determine the infinite limit

$\underset{x\to {\mathrm{\pi }}^{–}}{\lim }csc\left(x\right)$

 

 

12. Determine the infinite limit.

$\underset{x\to 3^{+}}{\lim }\frac{x^2–3x}{x^2–6x+9}$